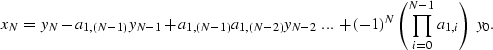
The stability of non-stationary inverse filtering

A filter is stable if any bounded input produces a bounded output Robinson and Treitel (1980). Therefore, to prove that inverse filtering with a class of filters is stable, we have to demonstrate that all possible members of the class have bounded outputs for all bounded inputs. On the other hand to show that a class of filters is not stable, we just need to find a single example where a bounded input produces an unbounded output.

The stability of stationary recursive inverse filtering depends on the phase of the causal filter: if (and only if) the filter is minimum phase, then its inverse filter is stable. This raises the question: is non-stationary inverse filtering stable if all filters contained in the filter-bank are minimum-phase?

For the case of inverse filtering with a two-point filter (N_a=2), equation (9) reduces to x₀=y₀, and the following formula for k>0:

x_k = y_k - a_1,(k-1) x_k-1.

Recursive substitution then produces an explicit formula for elements of ${\bf x}$ in terms of elements of ${\bf y}$:

$$x_N = y_N - a_{1,(N-1)} y_{N-1} + a_{1,(N-1)} a_{1,(N-2)} y_... ...... \; + (-1)^N \left( \prod_{i=0}^{N-1} a_{1,i} \right) \;y_0.$$ (125)

For stability analysis, we need to understand how the above series behaves as $N \to \infty$.If the filters, ${\bf a}_i$, are all minimum phase, and there exists a real number, $\kappa$, such that $\vert a_{1,i}\vert \leq \kappa <1$ for all i, then

$$\prod_{i=0}^{N-1} a_{1,i} \leq \kappa^N.$$ (126)

The above series will therefore converge, and stability is guaranteed. Furthermore, this proof can easily be extended to gapped two-point minimum-phase non-stationary filters, which correspond to matrices with ones on the main diagonal, and variable coefficients whose magnitude is less than one on a secondary diagonal.

There is a larger class ($N_a \geq 3$) of stable non-stationary recursive filters that can be obtained by repeatedly multiplying stable bidiagonal matrices. However, given a general non-stationary filter matrix, there is no straightforward way to determine whether it is a member of this stable class. In fact, it is relatively easy to find an example filter-bank consisting of minimum-phase individual filters whose recursive output is unbounded for finite input. Consider the filter-bank, ${\bf f}$, consisting of minimum-phase filters,

$$\begin{eqnarray} {\bf f}_{0,2,4...} & = & (1 \;\; -0.9 \;\; 0), \;\; {\rm and}\n... ...5...} & = & (1 \;\; 0.8) * (1 \;\; 0.8) = (1 \;\; 1.6 \;\; 0.64).\end{eqnarray}$$ (127)

Figure  shows the impulse response of non-stationary inverse filtering with this filter: clearly an unstable process.

 

one Figure 1 Impulsive input (a) and response (b) to non-stationary filtering with filter-bank defined in equation ().

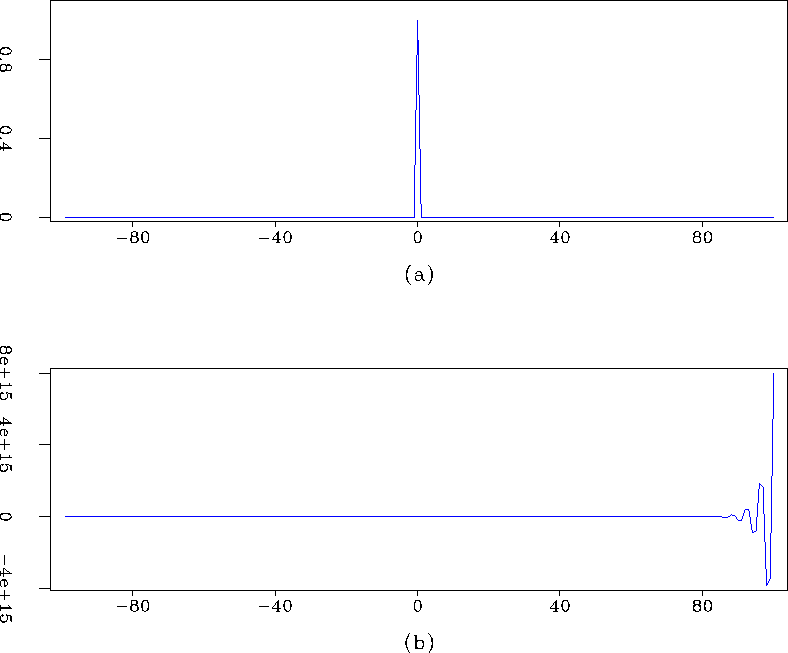The instability stems from the fact that as N increases, so does the number of boundaries between different filters. Such rapid non-stationary filter variations, as in the example above, are pathological in the context of seismic applications, where filters are typically quasi-stationary. For these applications instability is rarely observed; however, we must be aware that we are not dealing with an unconditionally stable operator, and instability may rear its ugly head from time-to-time.