![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) decomposes exploding-reflector modeling by
wavefield extrapolation into a spraying operator,
) decomposes exploding-reflector modeling by
wavefield extrapolation into a spraying operator,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) confirms this by displaying the
frequency-domain response of cascaded modeling and migration
(
confirms this by displaying the
frequency-domain response of cascaded modeling and migration
(
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) decomposes exploding-reflector modeling by
wavefield extrapolation into a spraying operator,
) decomposes exploding-reflector modeling by
wavefield extrapolation into a spraying operator,
![]() , followed by an
extrapolation/recording operator,
, followed by an
extrapolation/recording operator, ![]() , so that
, so that
| (80) | ||
| (81) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
,
If the approximation that ![]() is
indeed valid, then amplitude problems on
zero-offset migrations must be associated with the two-way wave
propagation rather than the exploding-reflector migration.
To test the validity of this conjecture, I can generate
exploding-reflector and genuine zero-offset seismograms and compare
the results of exploding-reflector migration on the two datasets.
is
indeed valid, then amplitude problems on
zero-offset migrations must be associated with the two-way wave
propagation rather than the exploding-reflector migration.
To test the validity of this conjecture, I can generate
exploding-reflector and genuine zero-offset seismograms and compare
the results of exploding-reflector migration on the two datasets.
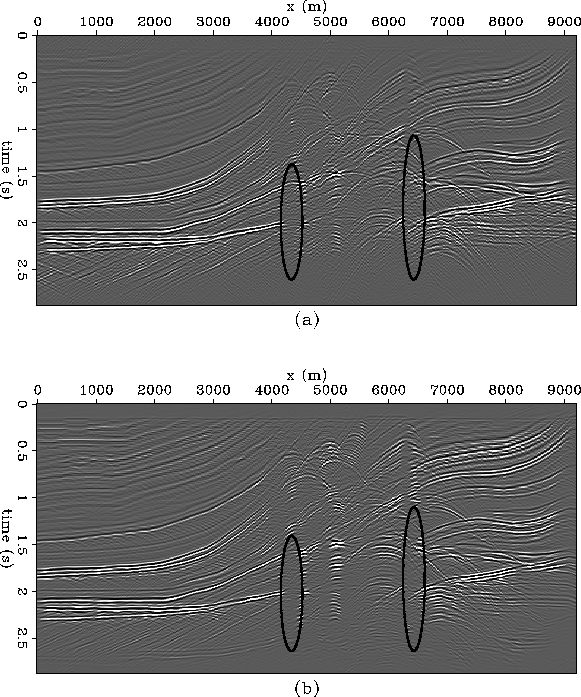
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares exploding-reflector data with
true zero-offset data. I generated the two datasets by running the
adjoint of exploding-reflector and shot-profile downward continuation
migration algorithms respectively.
Kinematically they are similar; however, vertical amplitude streaking
is much more apparent in the true zero-offset section.
Field datasets, such as the stacked section shown in
Figure
compares exploding-reflector data with
true zero-offset data. I generated the two datasets by running the
adjoint of exploding-reflector and shot-profile downward continuation
migration algorithms respectively.
Kinematically they are similar; however, vertical amplitude streaking
is much more apparent in the true zero-offset section.
Field datasets, such as the stacked section shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , often contain vertical amplitude
streaks. Such streaks often pose a dilemma for a processing
geophysicist as to how they should be correctly treated.
, often contain vertical amplitude
streaks. Such streaks often pose a dilemma for a processing
geophysicist as to how they should be correctly treated.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
|
illumexamples
Figure 5 Stacked section from the Mobil AVO dataset Clapp (1999). Vertical streaking is visible throughout the section. |  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
An even more interesting picture emerges when the two modeled datasets
are migrated (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with an exploding-reflector
migration algorithm. The exploding-reflector data migrates nearly
perfectly. Whereas the high amplitude streaks in the true zero-offset
dataset migrate into the commonly seen ``migration-smile'' artifacts.
) with an exploding-reflector
migration algorithm. The exploding-reflector data migrates nearly
perfectly. Whereas the high amplitude streaks in the true zero-offset
dataset migrate into the commonly seen ``migration-smile'' artifacts.
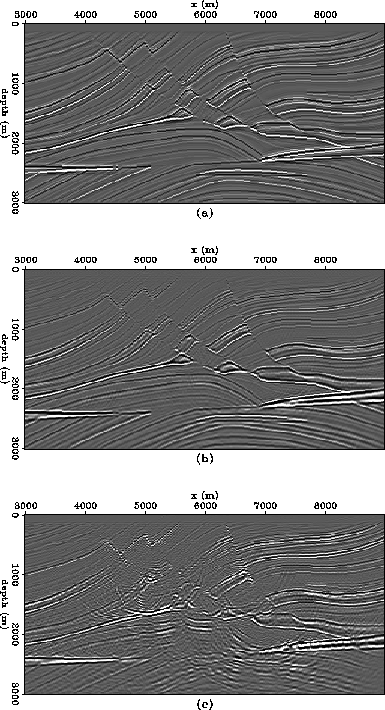 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (a), and panel (c) shows the
reflectivity estimate obtained by migrating the zero-offset data from
Figure
(a), and panel (c) shows the
reflectivity estimate obtained by migrating the zero-offset data from
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (b).
(b).
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)