




Next: Conclusions
Up: Regularizing reflection seismic data
Previous: 3-D data regularization with
Missing or under-sampled shot records are a common example of data
irregularity Crawley (2000). The offset continuation
approach can be easily modified to work in the shot record domain.
With the change of variables s = y - h, where s is the shot
location, the frequency-domain equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) transforms to
the equation
) transforms to
the equation
| 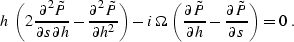 |
(133) |
Unlike equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which is second-order in the
propagation variable h, equation (
), which is second-order in the
propagation variable h, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) contains only
first-order derivatives in s. We can formally write its solution
for the initial conditions at s=s1 in the form of a phase-shift
operator:
) contains only
first-order derivatives in s. We can formally write its solution
for the initial conditions at s=s1 in the form of a phase-shift
operator:
| ![\begin{displaymath}
\widehat{\widehat{P}}(s_2) = \widehat{\widehat{P}}(s_1)\,
\...
...1\right)\,
\frac{k_h\,h-\Omega}{2\,k_h\,h-\Omega}\right]}\;,
\end{displaymath}](img264.gif) |
(134) |
where the wavenumber kh corresponds to the half-offset h.
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is in the mixed offset-wavenumber
domain and, therefore, not directly applicable in practice. However,
we can use it as an intermediate step in designing a
finite-difference shot continuation filter. Analogously to the cases
of plane-wave destruction and offset continuation, shot continuation
leads us to the rational filter
) is in the mixed offset-wavenumber
domain and, therefore, not directly applicable in practice. However,
we can use it as an intermediate step in designing a
finite-difference shot continuation filter. Analogously to the cases
of plane-wave destruction and offset continuation, shot continuation
leads us to the rational filter
| 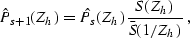 |
(135) |
The filter is non-stationary, because the coefficients of S(Zh)
depend on the half-offset h. We can find them by the Taylor
expansion of the phase-shift equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) around
zero wavenumber kh. For the case of the half-offset sampling
equal to the shot sampling, the simplest three-point filter is
constructed with three terms of the Taylor expansion. It takes the
form
) around
zero wavenumber kh. For the case of the half-offset sampling
equal to the shot sampling, the simplest three-point filter is
constructed with three terms of the Taylor expansion. It takes the
form
| 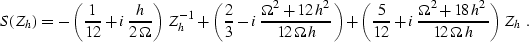 |
(136) |
Let us consider the problem of doubling the shot density. If we use
two neighboring shot records to find the missing record between
them, the problem reduces to the least-squares system
| ![\begin{displaymath}
\left[\begin{array}
{c}
\bold{S} \\ \bold{\bar{S}}
\end{...
...{p}_{s-1} \\ \bold{S}\,\bold{p}_{s+1}
\end{array}\right]\;,
\end{displaymath}](img267.gif) |
(137) |
where 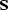 denotes convolution with the numerator of
equation (
denotes convolution with the numerator of
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
), 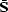 denotes convolution
with the corresponding denominator,
denotes convolution
with the corresponding denominator, 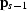 and
and
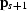 represent the known shot gathers, and
represent the known shot gathers, and 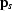 represents the gather that we want to estimate. The least-squares
solution of system (
represents the gather that we want to estimate. The least-squares
solution of system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) takes the form
) takes the form
| 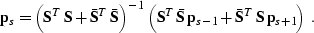 |
(138) |
If we choose the three-point filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to construct
the operators
) to construct
the operators 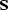 and
and 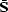 , then the inverted
matrix in equation (
, then the inverted
matrix in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will have five non-zero
diagonals. It can be efficiently inverted with a direct banded
matrix solver using the LDLT decomposition Golub and Van Loan (1996). Since
the matrix does not depend on the shot location, we can perform the
decomposition once for every frequency so that only a triangular
matrix inversion will be needed for interpolating each new shot.
This leads to an extremely efficient algorithm for interpolating
intermediate shot records.
) will have five non-zero
diagonals. It can be efficiently inverted with a direct banded
matrix solver using the LDLT decomposition Golub and Van Loan (1996). Since
the matrix does not depend on the shot location, we can perform the
decomposition once for every frequency so that only a triangular
matrix inversion will be needed for interpolating each new shot.
This leads to an extremely efficient algorithm for interpolating
intermediate shot records.
Sometimes, two neighboring shot gathers do not fully constrain the
intermediate shot. In order to add an additional constraint, I
include a regularization term in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), as
follows:
), as
follows:
| 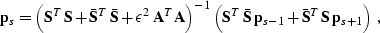 |
(139) |
where 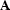 represents convolution with a three-point
prediction-error filter (PEF), and
represents convolution with a three-point
prediction-error filter (PEF), and  is a scaling
coefficient. The appropriate PEF can be estimated from
is a scaling
coefficient. The appropriate PEF can be estimated from
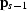 and
and 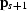 using Burg's algorithm
Burg (1972, 1975); Claerbout (1976). A
three-point filter leads does not break the five-diagonal structure
of the inverted matrix. The PEF regularization attempts to preserve
offset dip spectrum in the under-constrained parts of the estimated
shot gather.
using Burg's algorithm
Burg (1972, 1975); Claerbout (1976). A
three-point filter leads does not break the five-diagonal structure
of the inverted matrix. The PEF regularization attempts to preserve
offset dip spectrum in the under-constrained parts of the estimated
shot gather.
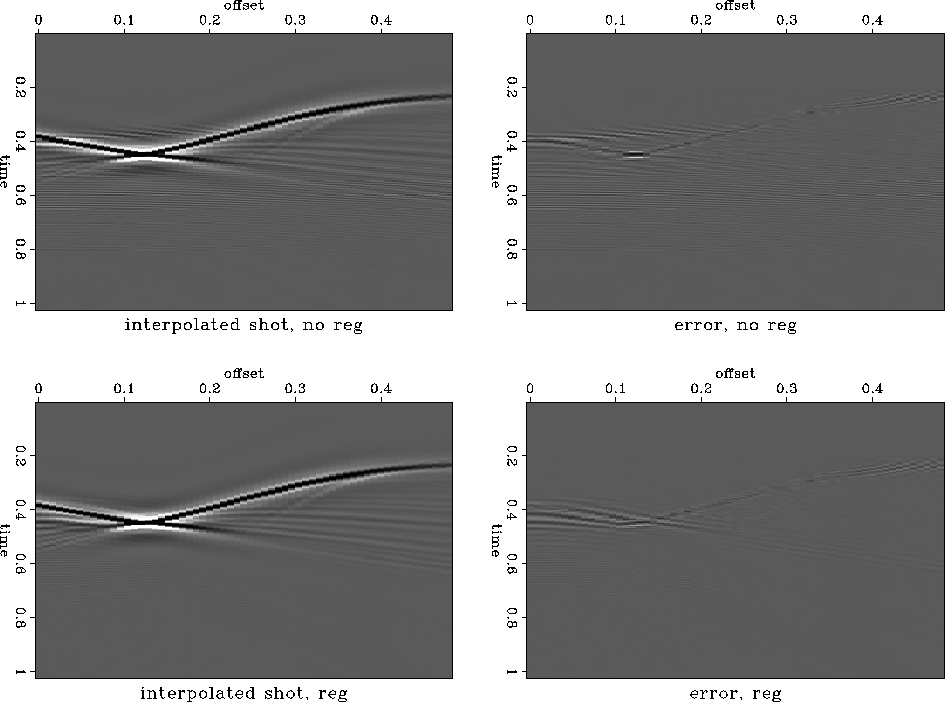
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of a shot interpolation
experiment using the constant-velocity synthetic from
Figure
shows the result of a shot interpolation
experiment using the constant-velocity synthetic from
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In this experiment, I removed one of the
shot gathers from the original data and interpolated it back using
equation (
. In this experiment, I removed one of the
shot gathers from the original data and interpolated it back using
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Subtracting the true shot gather from
the reconstructed one shows a very insignificant error, which is
further reduced by using the PEF regularization (right plots in
Figure
). Subtracting the true shot gather from
the reconstructed one shows a very insignificant error, which is
further reduced by using the PEF regularization (right plots in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The two neighboring shot gathers used in
this experiment are shown in the top plots of
Figure
). The two neighboring shot gathers used in
this experiment are shown in the top plots of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . For comparison, the bottom plots in
Figure
. For comparison, the bottom plots in
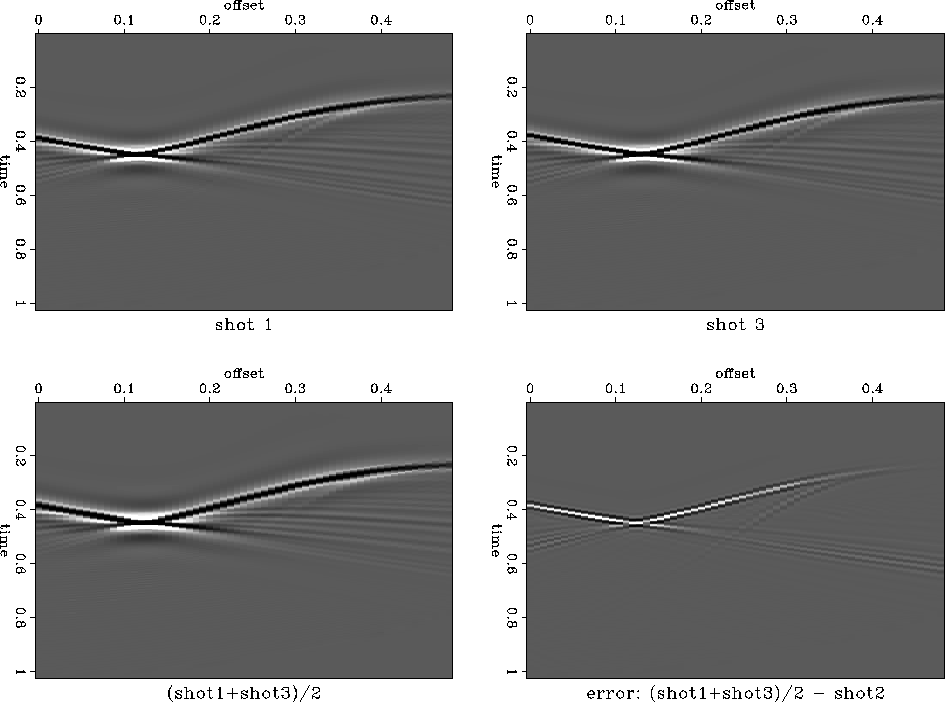
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the simple average of the two shot
gathers and its corresponding prediction error. As expected, the
error is significantly larger than the error of the shot
continuation. An interpolation scheme based on local dips in the shot
direction would probably achieve a better result, but it is
generally much more expensive than the shot continuation scheme
introduced above.
show the simple average of the two shot
gathers and its corresponding prediction error. As expected, the
error is significantly larger than the error of the shot
continuation. An interpolation scheme based on local dips in the shot
direction would probably achieve a better result, but it is
generally much more expensive than the shot continuation scheme
introduced above.
shot3
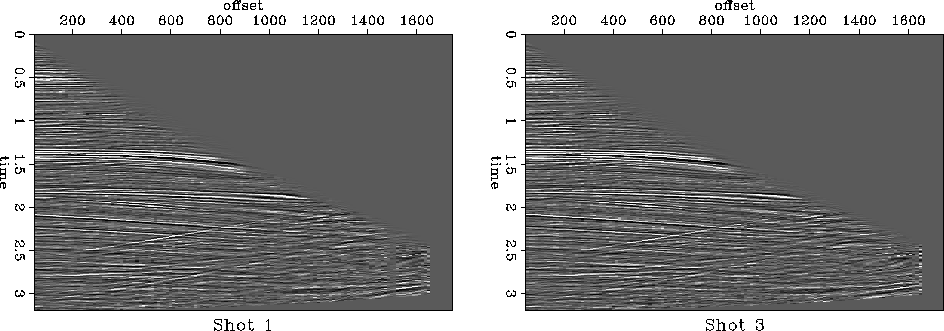
Figure 38 Top: Two synthetic shot gathers
used for the shot interpolation experiment. An NMO correction has
been applied. Bottom: simple average of the two shot gathers
(left) and its prediction error (right).
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





shotin
Figure 39 Synthetic shot interpolation
results. Left: interpolated shot gathers. Right: prediction errors
(the differences between interpolated and true shot gathers),
plotted on the same scale. Top: without regularization. Bottom:
with PEF regularization.





A similar experiment with real data from a North Sea marine dataset
is reported in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . I removed and
reconstructed a shot gather from the two neighboring gathers shown
in Figure
. I removed and
reconstructed a shot gather from the two neighboring gathers shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The lower parts of the gathers are
complicated by salt dome reflections and diffractions with
conflicting dips. The simple average of the two input shot gathers
(bottom plots in Figure
. The lower parts of the gathers are
complicated by salt dome reflections and diffractions with
conflicting dips. The simple average of the two input shot gathers
(bottom plots in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) works reasonably well
for nearly flat reflection events but fails to predict the position
of the back-scattered diffractions events. The shot continuation
method works well for both types of events (top plots in
Figure
) works reasonably well
for nearly flat reflection events but fails to predict the position
of the back-scattered diffractions events. The shot continuation
method works well for both types of events (top plots in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). There is some small and random residual
error, possibly caused by local amplitude variations.
). There is some small and random residual
error, possibly caused by local amplitude variations.
elfshot3
Figure 40 Two real marine shot gathers
used for the shot interpolation experiment. An NMO correction has
been applied.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





elfshotin
Figure 41 Real-data shot interpolation
results. Top: interpolated shot gather (left) and its prediction
error (right). Bottom: simple average of the two input shot
gathers (left) and its prediction error (right).










Next: Conclusions
Up: Regularizing reflection seismic data
Previous: 3-D data regularization with
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) transforms to
the equation
) transforms to
the equation
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) transforms to
the equation
) transforms to
the equation
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which is second-order in the
propagation variable h, equation (
), which is second-order in the
propagation variable h, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) contains only
first-order derivatives in s. We can formally write its solution
for the initial conditions at s=s1 in the form of a phase-shift
operator:
) contains only
first-order derivatives in s. We can formally write its solution
for the initial conditions at s=s1 in the form of a phase-shift
operator:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is in the mixed offset-wavenumber
domain and, therefore, not directly applicable in practice. However,
we can use it as an intermediate step in designing a
finite-difference shot continuation filter. Analogously to the cases
of plane-wave destruction and offset continuation, shot continuation
leads us to the rational filter
) is in the mixed offset-wavenumber
domain and, therefore, not directly applicable in practice. However,
we can use it as an intermediate step in designing a
finite-difference shot continuation filter. Analogously to the cases
of plane-wave destruction and offset continuation, shot continuation
leads us to the rational filter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) around
zero wavenumber kh. For the case of the half-offset sampling
equal to the shot sampling, the simplest three-point filter is
constructed with three terms of the Taylor expansion. It takes the
form
) around
zero wavenumber kh. For the case of the half-offset sampling
equal to the shot sampling, the simplest three-point filter is
constructed with three terms of the Taylor expansion. It takes the
form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
), ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) takes the form
) takes the form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to construct
the operators
) to construct
the operators ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will have five non-zero
diagonals. It can be efficiently inverted with a direct banded
matrix solver using the LDLT decomposition Golub and Van Loan (1996). Since
the matrix does not depend on the shot location, we can perform the
decomposition once for every frequency so that only a triangular
matrix inversion will be needed for interpolating each new shot.
This leads to an extremely efficient algorithm for interpolating
intermediate shot records.
) will have five non-zero
diagonals. It can be efficiently inverted with a direct banded
matrix solver using the LDLT decomposition Golub and Van Loan (1996). Since
the matrix does not depend on the shot location, we can perform the
decomposition once for every frequency so that only a triangular
matrix inversion will be needed for interpolating each new shot.
This leads to an extremely efficient algorithm for interpolating
intermediate shot records.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), as
follows:
), as
follows:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of a shot interpolation
experiment using the constant-velocity synthetic from
Figure
shows the result of a shot interpolation
experiment using the constant-velocity synthetic from
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In this experiment, I removed one of the
shot gathers from the original data and interpolated it back using
equation (
. In this experiment, I removed one of the
shot gathers from the original data and interpolated it back using
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Subtracting the true shot gather from
the reconstructed one shows a very insignificant error, which is
further reduced by using the PEF regularization (right plots in
Figure
). Subtracting the true shot gather from
the reconstructed one shows a very insignificant error, which is
further reduced by using the PEF regularization (right plots in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The two neighboring shot gathers used in
this experiment are shown in the top plots of
Figure
). The two neighboring shot gathers used in
this experiment are shown in the top plots of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . For comparison, the bottom plots in
Figure
. For comparison, the bottom plots in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the simple average of the two shot
gathers and its corresponding prediction error. As expected, the
error is significantly larger than the error of the shot
continuation. An interpolation scheme based on local dips in the shot
direction would probably achieve a better result, but it is
generally much more expensive than the shot continuation scheme
introduced above.
show the simple average of the two shot
gathers and its corresponding prediction error. As expected, the
error is significantly larger than the error of the shot
continuation. An interpolation scheme based on local dips in the shot
direction would probably achieve a better result, but it is
generally much more expensive than the shot continuation scheme
introduced above.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . I removed and
reconstructed a shot gather from the two neighboring gathers shown
in Figure
. I removed and
reconstructed a shot gather from the two neighboring gathers shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The lower parts of the gathers are
complicated by salt dome reflections and diffractions with
conflicting dips. The simple average of the two input shot gathers
(bottom plots in Figure
. The lower parts of the gathers are
complicated by salt dome reflections and diffractions with
conflicting dips. The simple average of the two input shot gathers
(bottom plots in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) works reasonably well
for nearly flat reflection events but fails to predict the position
of the back-scattered diffractions events. The shot continuation
method works well for both types of events (top plots in
Figure
) works reasonably well
for nearly flat reflection events but fails to predict the position
of the back-scattered diffractions events. The shot continuation
method works well for both types of events (top plots in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). There is some small and random residual
error, possibly caused by local amplitude variations.
). There is some small and random residual
error, possibly caused by local amplitude variations.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
