Next: Regularizing local plane waves
Up: Regularizing smooth data with
Previous: Finite differences and spectral
I chose an environmental Galilee dataset Claerbout (1999); Fomel and Claerbout (1995)
for a simple illustration of smooth data regularization. The data were
collected on a bottom sounding survey of the Sea of Galilee in Israel
Ben-Avraham et al. (1990). The data contain a number of noisy, erroneous and
inconsistent measurements, which present a challenge for the
traditional estimation methods.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the data after a nearest-neighbor binning
to a regular grid. The data were then passed to an interpolation
program to fill the empty bins. The results (for different values of
shows the data after a nearest-neighbor binning
to a regular grid. The data were then passed to an interpolation
program to fill the empty bins. The results (for different values of
 ) are shown in Figures
) are shown in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Interpolation with the minimum-phase Laplacian (
.
Interpolation with the minimum-phase Laplacian (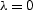 ) creates a
relatively smooth interpolation surface but plants artificial
``hills'' around the edge of the sea. This effect is caused by large
gradient changes and is similar to the sidelobe effect in the
one-dimensional example (Figure
) creates a
relatively smooth interpolation surface but plants artificial
``hills'' around the edge of the sea. This effect is caused by large
gradient changes and is similar to the sidelobe effect in the
one-dimensional example (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). It is clearly seen in
the cross-section plots in Figure
). It is clearly seen in
the cross-section plots in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The abrupt
gradient change is a typical case of a shelf break. It is caused by a
combination of sedimentation and active rifting. Interpolation with
the helix derivative (
. The abrupt
gradient change is a typical case of a shelf break. It is caused by a
combination of sedimentation and active rifting. Interpolation with
the helix derivative (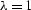 ) is free from the sidelobe
artifacts, but it also produces an undesirable non-smooth behavior in
the middle part of the image. As in the one-dimensional example,
intermediate tension allows us to achieve a compromise: smooth
interpolation in the middle and constrained behavior at the sides of
the sea bottom.
) is free from the sidelobe
artifacts, but it also produces an undesirable non-smooth behavior in
the middle part of the image. As in the one-dimensional example,
intermediate tension allows us to achieve a compromise: smooth
interpolation in the middle and constrained behavior at the sides of
the sea bottom.
mesh
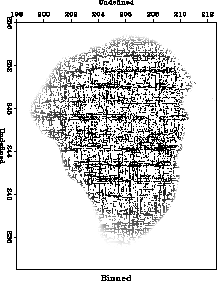
Figure 6 The Sea of Galilee dataset after
a nearest-neighbor binning. The binned data is used as an input for
the missing data interpolation program.
|
|  |




 gal
gal
Figure 7 The Sea of Galilee dataset after
missing data interpolation with helical preconditioning. Different
plots correspond to different values of the tension parameter. An
east-west derivative filter was applied to illuminate the surface.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)




 cross
cross
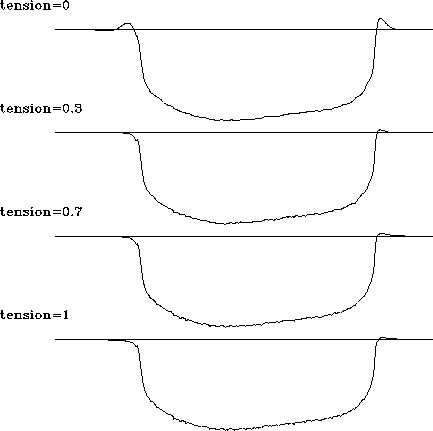
Figure 8 Cross-sections of the Sea of
Galilee dataset after missing-data interpolation with helical
preconditioning. Different plots correspond to different values of
the tension parameter.





Smooth surfaces are rarely encountered in the practice of seismic
exploration. In the next section, I develop a regularization operator
suitable for characterizing more typical models of seismic data.





Next: Regularizing local plane waves
Up: Regularizing smooth data with
Previous: Finite differences and spectral
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the data after a nearest-neighbor binning
to a regular grid. The data were then passed to an interpolation
program to fill the empty bins. The results (for different values of
shows the data after a nearest-neighbor binning
to a regular grid. The data were then passed to an interpolation
program to fill the empty bins. The results (for different values of
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Interpolation with the minimum-phase Laplacian (
.
Interpolation with the minimum-phase Laplacian (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). It is clearly seen in
the cross-section plots in Figure
). It is clearly seen in
the cross-section plots in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The abrupt
gradient change is a typical case of a shelf break. It is caused by a
combination of sedimentation and active rifting. Interpolation with
the helix derivative (
. The abrupt
gradient change is a typical case of a shelf break. It is caused by a
combination of sedimentation and active rifting. Interpolation with
the helix derivative (

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)