Next: SeaBeam water bottom
Up: Two-dimensional environmental data examples
Previous: Two-dimensional environmental data examples
The first test dataset contains rainfall measurements from Switzerland
on the 8th of May 1986. The dataset was used in the Spatial
Interpolation Comparison Dubois (1999) for comparing different spatial
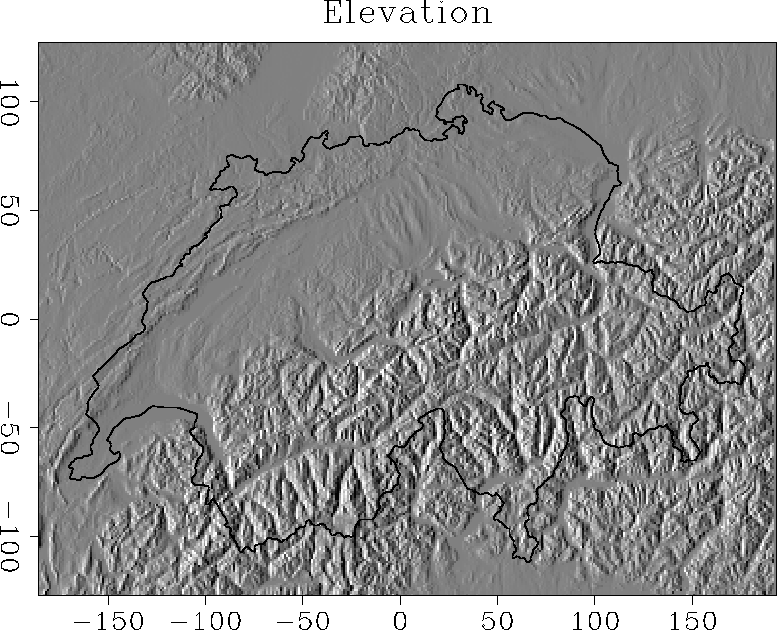
interpolation methods. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the data area: the
Digital Elevation Model of Switzerland and the country's
borders
shows the data area: the
Digital Elevation Model of Switzerland and the country's
borders![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) . A total of 467
rainfall measurements were taken. A subset of randomly selected 100
measurements was used in the 1997 Spatial Interpolation Comparison in
order to compare the results with the known data.
Figure
. A total of 467
rainfall measurements were taken. A subset of randomly selected 100
measurements was used in the 1997 Spatial Interpolation Comparison in
order to compare the results with the known data.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the spatial location of the selected
data samples.
shows the spatial location of the selected
data samples.
elev
Figure 15 Digital Elevation Model of Switzerland
and the country's borders. The country borders are extracted from
the Digital Chart of the World (DCW) provided by ESRI.
|
|  |




 raindata
raindata
Figure 16 Left: data locations for all 467
measurements. Right: data locations for selected 100 measurements.





Rainfall level is generally a smoothly varying quantity. We cannot
expect it to be represented a priori by a simple function. Therefore,
it is reasonable to take the regularization operator  to be
a convolution with the Laplacian filter. The corresponding
preconditioning operator
to be
a convolution with the Laplacian filter. The corresponding
preconditioning operator  is then a deconvolution with the
minimum-phase Laplacian constructed in the previous section. The
interpolation result using the model-space regularization
scheme (
is then a deconvolution with the
minimum-phase Laplacian constructed in the previous section. The
interpolation result using the model-space regularization
scheme (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is shown in
Figure
) is shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The input irregular data were regularized
on a 376 by 253 grid, which corresponds to the digital elevation model
in Figure
. The input irregular data were regularized
on a 376 by 253 grid, which corresponds to the digital elevation model
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Similarly to what happens in the
one-dimensional synthetic examples, the solution converges steadily
but with a slow spread of information away from the known data points.
It takes about 10,000 iterations to achieve full convergence.
Figure
. Similarly to what happens in the
one-dimensional synthetic examples, the solution converges steadily
but with a slow spread of information away from the known data points.
It takes about 10,000 iterations to achieve full convergence.
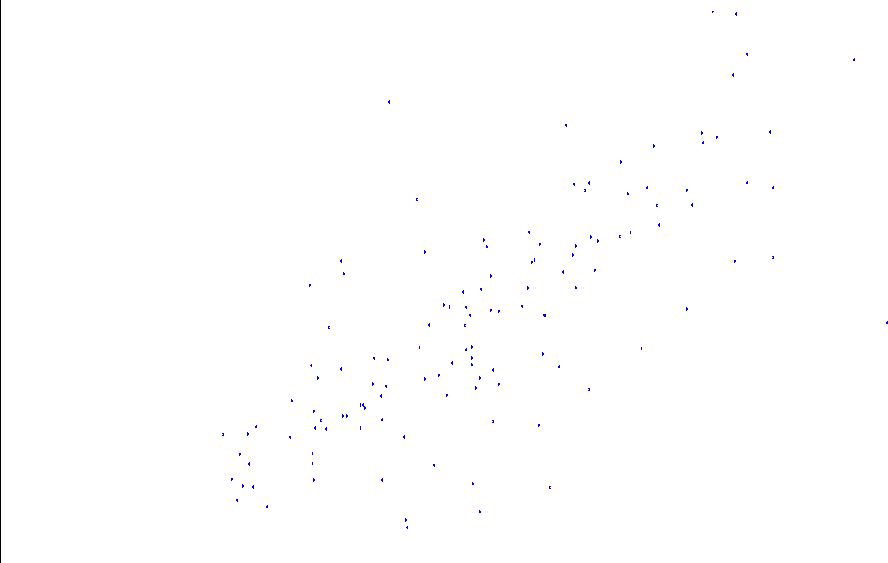
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is a correlation plot of the observed and
interpolated data points for the 367 points that were not used in the
interpolation experiment. If we take into account the fairly
unpredictable distribution of rainfall, the correlation is relatively
good in comparison with analogous results of the Spatial Interpolation
Contest Dubois (1999).
is a correlation plot of the observed and
interpolated data points for the 367 points that were not used in the
interpolation experiment. If we take into account the fairly
unpredictable distribution of rainfall, the correlation is relatively
good in comparison with analogous results of the Spatial Interpolation
Contest Dubois (1999).
lapinter
Figure 17 Rainfall data after model-space
regularization with 10, 100, 1000, and 10000 iterations.





lapstat
Figure 18 Correlation between observed and
predicted rainfall data values.
|
|  |





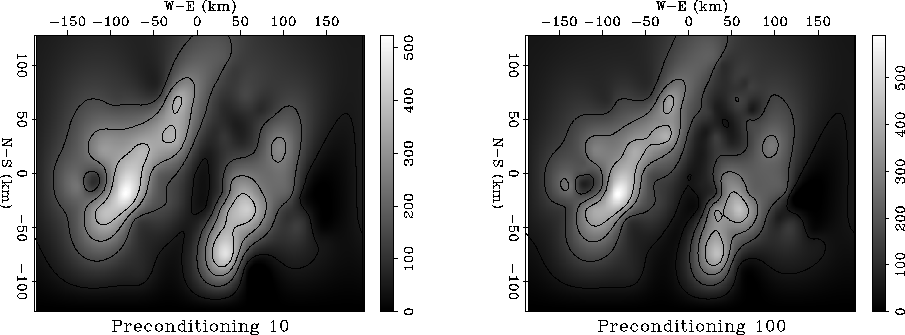
The result of applying recursive filter preconditioning with the
minimum-phase Laplacian operator is shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Full convergence is achieved after only
100 iterations. The result after 10 iterations (the left plot in
Figure
. Full convergence is achieved after only
100 iterations. The result after 10 iterations (the left plot in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is already close to the final solution.
Recursive preconditioning speeded up the iteration count by a factor
of 1000. The actual gain in execution time is several times smaller
because of the correspondingly longer filter, but it is still
impressively large.
) is already close to the final solution.
Recursive preconditioning speeded up the iteration count by a factor
of 1000. The actual gain in execution time is several times smaller
because of the correspondingly longer filter, but it is still
impressively large.
precinter
Figure 19 Rainfall data after data-space
regularization (recursive filter preconditioning) with 10 and 100
iterations.










Next: SeaBeam water bottom
Up: Two-dimensional environmental data examples
Previous: Two-dimensional environmental data examples
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the data area: the
Digital Elevation Model of Switzerland and the country's
borders
shows the data area: the
Digital Elevation Model of Switzerland and the country's
borders![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) . A total of 467
rainfall measurements were taken. A subset of randomly selected 100
measurements was used in the 1997 Spatial Interpolation Comparison in
order to compare the results with the known data.
Figure
. A total of 467
rainfall measurements were taken. A subset of randomly selected 100
measurements was used in the 1997 Spatial Interpolation Comparison in
order to compare the results with the known data.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the spatial location of the selected
data samples.
shows the spatial location of the selected
data samples.