SYMMETRIES

Next we examine odd/even symmetries to see how they are affected in Fourier transform. The even part e_t of a signal b_t is defined as  

$$e_t \eq {b_t + b_{-t} \over 2}$$ (32)

The odd part is  

$$o_t \eq {b_t - b_{-t} \over 2}$$ (33)

By adding (32) and (33), we see that a function is the sum of its even and odd parts:  

$$b_t \eq e_t + o_t$$ (34)

Consider a simple, real, even signal such as (b_-1, b₀, b₁) = (1, 0, 1). Its transform $Z + 1/Z = e^{i\omega}+e^{-i\omega} = 2\cos \omega$is an even function of $\omega$, since $\cos \omega = \cos (-\omega)$.

Consider the real, odd signal (b_-1, b₀, b₁) = (-1, 0, 1). Its transform $Z - 1/Z = 2i\sin\omega$ is imaginary and odd, since $\sin \omega = -\sin(-\omega)$.

Likewise, the transform of the imaginary even function (i, 0, i) is the imaginary even function $i2 \cos \omega$.Finally, the transform of the imaginary odd function (-i, 0, i) is real and odd.

Let r and i refer to real and imaginary, e and o to even and odd, and lower-case and upper-case letters to time and frequency functions. A summary of the symmetries of Fourier transform is shown in Figure 10.

 

reRE Figure 10 Odd functions swap real and imaginary. Even functions do not get mixed up with complex numbers.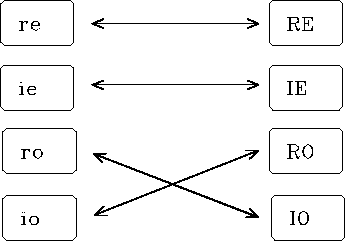

More elaborate signals can be made by adding together the three-point functions we have considered. Since sums of even functions are even, and so on, the diagram in Figure 10 applies to all signals. An arbitrary signal is made from these four parts only, i.e., the function has the form $b_t = ( {\rm re} + {\rm ro})_t + i ( {\rm ie} + {\rm io})_t$.On transformation of b_t, each of the four individual parts transforms according to the table.

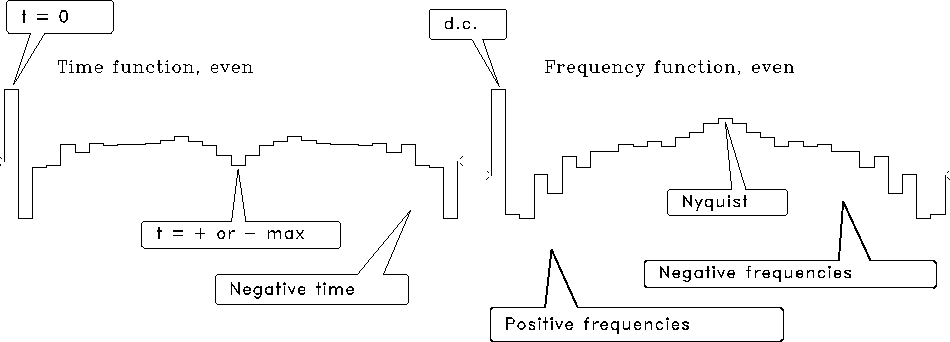
Most ``industry standard'' methods of Fourier transform set the zero frequency as the first element in the vector array holding the transformed signal, as implied by equation (26). This is a little inconvenient, as we saw a few pages back. The Nyquist frequency is then the first point past the middle of the even-length array, and the negative frequencies lie beyond. Figure 11 shows an example of an even function as it is customarily stored.

 

even
Figure 11 Even functions as customarily stored by ``industry standard'' FT programs.

EXERCISES:

1. You can learn about Fourier transformation by studying math equations in a book. You can also learn by experimenting with a program where you can ``draw'' a function in the time domain (or frequency domain) and instantly see the result in the other domain. The best way to learn about FT is to combine the above two methods. Spend at least an hour at the web site:

   http://sepwww.stanford.edu/oldsep/hale/FftLab.html

   which contains the interactive Java FT laboratory written by Dave Hale. This program applies equations (26) and (27).