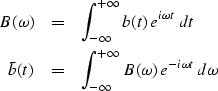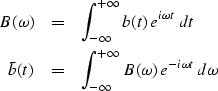Next: SYMMETRIES
Up: FT AS AN INVERTIBLE
Previous: Convolution in one domain...
Fourier analysis is widely used in mathematics, physics, and engineering
as a Fourier integral transformation pair:
| 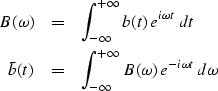 |
(30) |
| (31) |
These integrals correspond to the sums we are working with here
except for some minor details.
Books in electrical engineering redefine
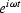 as
as
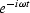 .That is like switching
.That is like switching 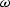 to
to 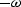 .Instead,
we have chosen the sign convention
of physics,
which is better for wave-propagation studies (as explained in IEI).
The infinite limits on the integrals
result from expressing the
Nyquist frequency
in radians/second as
.Instead,
we have chosen the sign convention
of physics,
which is better for wave-propagation studies (as explained in IEI).
The infinite limits on the integrals
result from expressing the
Nyquist frequency
in radians/second as 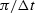 .Thus,
as
.Thus,
as 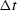 tends to zero,
the Fourier sum
tends to the integral.
It can be shown that
if a scaling divisor of
tends to zero,
the Fourier sum
tends to the integral.
It can be shown that
if a scaling divisor of 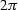 is introduced
into either (30) or (31),
then b(t) will equal
is introduced
into either (30) or (31),
then b(t) will equal 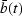 .
.EXERCISES:
-
Let B(Z) = 1 + Z + Z2 + Z3 + Z4.
Graph the coefficients of B(Z) as a function of the powers of Z.
Graph the coefficients of
![$\left[ B(Z) \right]^2$](img97.gif) .
. -
As
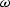 moves from zero to positive frequencies,
where is Z and which way does it rotate around the unit circle,
clockwise or counterclockwise?
moves from zero to positive frequencies,
where is Z and which way does it rotate around the unit circle,
clockwise or counterclockwise?
-
Identify locations
on the unit circle
of the following frequencies:
(1) the zero frequency,
(2) the Nyquist frequency,
(3) negative frequencies,
and
(4) a frequency sampled at 10 points per wavelength.
-
Sketch the amplitude spectrum of Figure 8
from 0 to
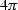 .
.





Next: SYMMETRIES
Up: FT AS AN INVERTIBLE
Previous: Convolution in one domain...
Stanford Exploration Project
3/1/2001