![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
Given an input X(Z) and an output Y(Z), we know that the spectra
of the two are the same, i.e.,
![]() .The existence of an infinitude of all-pass filters tells us
that an infinitude of wavelets can have the same spectrum.
Wave propagation without absorption is modeled by all-pass filters.
All-pass filters yield a waveform distortion
that can be corrected by methods discussed in chapter
.The existence of an infinitude of all-pass filters tells us
that an infinitude of wavelets can have the same spectrum.
Wave propagation without absorption is modeled by all-pass filters.
All-pass filters yield a waveform distortion
that can be corrected by methods discussed in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
The simplest example of an all-pass filter
is the delay operator ![]() itself.
Its phase as a function of
itself.
Its phase as a function of ![]() is simply
is simply ![]() .
.
A less trivial example of phase distortion
can be constructed from a single root
Zr, where Zr is an arbitrary complex number.
The ratio of any complex number to its complex conjugate,
say (x+iy)/(x-iy),
is of unit magnitude, because,
taking ![]() and
and ![]() ,the ratio is
,the ratio is ![]() .Thus, given a minimum-phase filter
.Thus, given a minimum-phase filter ![]() ,we can take its
conjugate
and make an all-pass filter P(Z) from the ratio
,we can take its
conjugate
and make an all-pass filter P(Z) from the ratio
![]() .A simple case is
.A simple case is
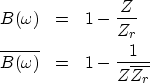 |
(45) | |
| (46) |
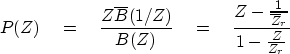 |
(47) |
|
disper
Figure 13 Examples of causal all-pass filters with real poles and zeros. These have high frequencies at the beginning and low frequencies at the end. | 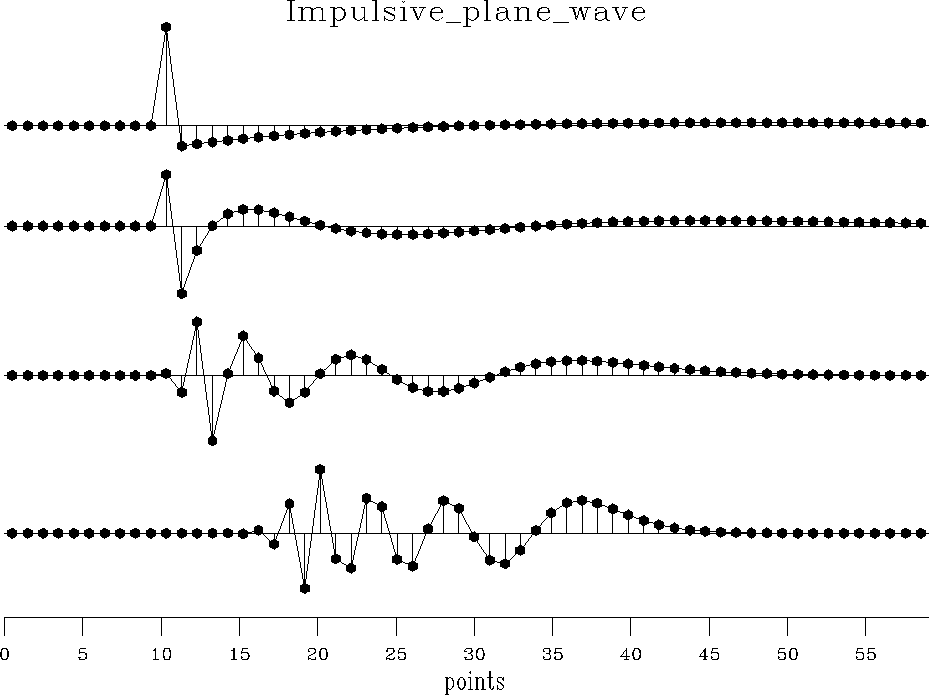 |
The denominator of equation (47) tells us
that we have a pole at Zr.
Let this location be ![]() .The numerator vanishes at
.The numerator vanishes at
| (48) |
The all-pass filter (47)
outputs a complex-valued signal, however.
To see real outputs, we must
handle the negative frequencies in the same way as the positive ones.
The filter (47) should be multiplied by another like itself
but with ![]() replaced by
replaced by ![]() ; i.e., with
Zr replaced by
; i.e., with
Zr replaced by ![]() .The result of this procedure is shown in Figure 14.
.The result of this procedure is shown in Figure 14.
 |
A general form for an all-pass filter is
![]() ,where A(Z) is an arbitrary minimum-phase filter.
That this form is valid can be verified by
checking that
,where A(Z) is an arbitrary minimum-phase filter.
That this form is valid can be verified by
checking that ![]() .
.
![]()