




Next: INTRODUCTION TO ALL-PASS FILTERS
Up: MINIMUM-PHASE FILTERS
Previous: Mechanical interpretation
Given an unknown filter B(Z), to understand its inverse,
we need to
factor B(Z) into two parts:
B(Z) = Bout(Z) Bin(Z), where Bout contains all the
roots outside the
unit circle and Bin contains all the roots inside.
Then the inverse of Bout
is expressed as a Taylor series about the origin,
and the inverse of Bin is expressed as a Taylor series about infinity.
The final expression for 1/B(Z)
is called a ``Laurent expansion'' for 1/B(Z),
and it converges on a ring including the unit circle.
Cases with zeros exactly on the unit circle present special problems.
For example, the differentiation filter (1-Z)
is the inverse of integration,
but the converse is not true,
because of the additive constant of integration.
EXERCISES:
-
Find the filter that is inverse to (2 - 5Z + 2Z2).
You may just
drop higher-order powers of Z, but an exact expression for the
coefficients of any power of Z is preferable.
(Partial fractions is a useful, though not a necessary, technique.)
Sketch the impulse response.
-
Describe a general method for determining A(Z) and B(Z) from a
Taylor series of
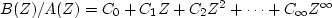 ,where B(Z) and A(Z) are polynomials of unknown degree n and m,
respectively.
Work out the case
,where B(Z) and A(Z) are polynomials of unknown degree n and m,
respectively.
Work out the case
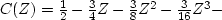
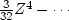 .Do not try this problem unless you are
familiar with determinants.
(HINT: identify coefficients of B(Z) = A(Z) C(Z).)
.Do not try this problem unless you are
familiar with determinants.
(HINT: identify coefficients of B(Z) = A(Z) C(Z).)





Next: INTRODUCTION TO ALL-PASS FILTERS
Up: MINIMUM-PHASE FILTERS
Previous: Mechanical interpretation
Stanford Exploration Project
10/21/1998