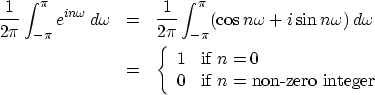Next: CORRELATION AND SPECTRA
Up: FOURIER AND Z-TRANSFORM
Previous: Complex roots
Fourier analysis is widely used in mathematics, physics, and engineering
as a Fourier integral transformation pair:
| 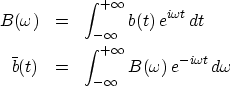 |
(26) |
| (27) |
These integrals correspond to the sums we are working with here
except for some minor details.
Books in electrical engineering redefine
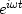 as
as
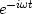 .That is like switching
.That is like switching  to
to 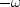 .Instead,
we have chosen the sign convention
of physics,
which is better for wave-propagation studies (as explained in IEI).
The infinite limits on the integrals
result from expressing the
Nyquist frequency
in radians/second as
.Instead,
we have chosen the sign convention
of physics,
which is better for wave-propagation studies (as explained in IEI).
The infinite limits on the integrals
result from expressing the
Nyquist frequency
in radians/second as 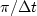 .Thus,
as
.Thus,
as 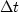 tends to zero,
the Fourier sum
tends to the integral.
When we reach equation (31) we will see that
if a scaling divisor of
tends to zero,
the Fourier sum
tends to the integral.
When we reach equation (31) we will see that
if a scaling divisor of 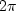 is introduced
into either (26) or (27), then
b(t) will equal
is introduced
into either (26) or (27), then
b(t) will equal 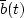 .
.
The Z-transform is always easy to make,
but the Fourier integral could be difficult to perform,
which is paradoxical,
because the transforms are really the same.
To make a Z-transform, we merely attach
powers of Z to successive data points.
When we have B(Z), we can refer to it either as a time
function or a frequency function.
If we graph the polynomial coefficients, then it is a time function.
It is a frequency function
if we evaluate and graph the polynomial 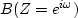 for
various frequencies
for
various frequencies  .
.
If the Z-transform amounts to attaching powers of Z to successive
points of a time function,
then the inverse Z-transform
must be merely
identifying coefficients of various powers of Z with different points in time.
How can this mere ``identification of coefficients'' be the same as the
apparently more complicated operation of inverse Fourier integration?
Let us see.
The
inverse Fourier integral
(27)
for integer values of time is
| 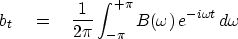 |
(28) |
Substituting (21) into (28), we get
| 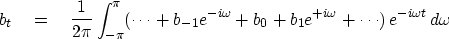 |
(29) |
Since sinusoids have as much area above the axis as below,
the integration of
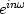 over
over 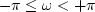 gives zero unless n = 0, that is,
gives zero unless n = 0, that is,
| 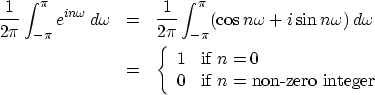 |
|
| (30) |
Of all the terms in the integrand (29),
we see from (30) that only the term
with bt will contribute to the integral;
all the rest oscillate and cancel.
In other words, it is only the coefficient of Z
to the zero power that contributes to the integral,
so (29) reduces to
| 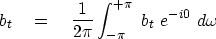 |
(31) |
This shows how inverse Fourier transformation is just like identifying
coefficients of powers of Z.
It also shows why the scale factor in equation (28) is 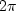 .
.EXERCISES:
-
Let B(Z) = 1 + Z + Z2 + Z3 + Z4.
Graph the coefficients of B(Z) as a function of the powers of Z.
Graph the coefficients of
![$\left[ B(Z) \right]^2$](img95.gif) .
. -
As
 moves from zero to positive frequencies,
where is Z and which way does it rotate around the unit circle,
clockwise or counterclockwise?
moves from zero to positive frequencies,
where is Z and which way does it rotate around the unit circle,
clockwise or counterclockwise?
-
Identify locations
on the unit circle
of the following frequencies:
(1) the zero frequency,
(2) the Nyquist frequency,
(3) negative frequencies,
and
(4) a frequency sampled at 10 points per wavelength.
-
Given numerical constants
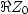 and
and 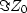 ,derive
,derive 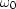 and
and  .
. -
Sketch the amplitude spectrum of Figure 9
from 0 to
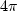 .
.





Next: CORRELATION AND SPECTRA
Up: FOURIER AND Z-TRANSFORM
Previous: Complex roots
Stanford Exploration Project
10/21/1998
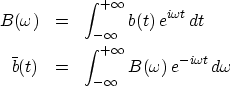
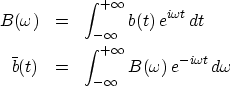
![]() for
various frequencies
for
various frequencies ![]() .
.