The way to avoid complex-valued signals
is to handle negative frequency ![]() the same way we handle
the same way we handle ![]() .To do this we use a filter with
two roots,
one at
.To do this we use a filter with
two roots,
one at ![]() and one at
and one at ![]() .The filter (1+iZ)(1-iZ)= 1+Z2
has real-valued time-domain coefficients,
namely, (1,0,1).
The factor (1+iZ) vanishes when Z=i or
.The filter (1+iZ)(1-iZ)= 1+Z2
has real-valued time-domain coefficients,
namely, (1,0,1).
The factor (1+iZ) vanishes when Z=i or ![]() ,and (1-iZ) vanishes at
,and (1-iZ) vanishes at ![]() .Notice what happens when the filter (1,0,1)
is convolved with the time series
.Notice what happens when the filter (1,0,1)
is convolved with the time series
![]() :the output is zero at all times.
This is because bt is a sinusoid
at the half-Nyquist frequency
:the output is zero at all times.
This is because bt is a sinusoid
at the half-Nyquist frequency ![]() ,and the filter (1,0,1) has zeros at plus and minus half-Nyquist.
,and the filter (1,0,1) has zeros at plus and minus half-Nyquist.
Let us work out the general case for a root anywhere in the complex plane. Let the root Z0 be decomposed into its real and imaginary parts:
| (22) |
| (23) |
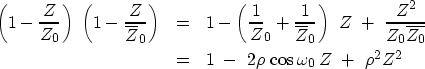 |
(24) | |
| (25) |
Recall that to keep the filter response real,
any root on the positive ![]() -axis
must have a twin on the negative
-axis
must have a twin on the negative ![]() -axis.
In the figures I show here,
the negative axis is not plotted, so we must remember the twin.
Figure 10 shows a discrete approximation
to the second derivative.
-axis.
In the figures I show here,
the negative axis is not plotted, so we must remember the twin.
Figure 10 shows a discrete approximation
to the second derivative.
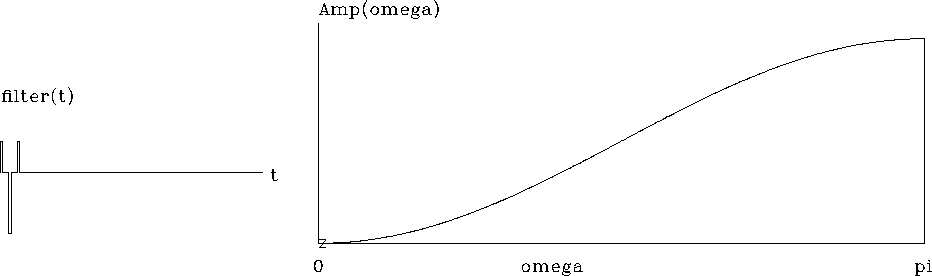 |
It is like (1-Z)2, but since both its roots are in the same place at Z=1, I pushed them a little distance apart, one going to positive frequencies and one to negative.