




Next: Processing possibilities
Up: INTERVAL VELOCITY BY LINEAR
Previous: Common-midpoint Snell coordinates
The chain rule for partial differentiation gives
| ![\begin{displaymath}
\left[ \
\matrix { \partial_t \cr \partial_g \cr \partial_s...
... \partial_y
\cr \partial_{{h}' } \cr \partial_{\tau} }
\right]\end{displaymath}](img128.gif) |
(66) |
In our usual notation
the Fourier representation of the
time derivative 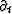 is
is 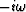 .Likewise,
.Likewise, 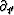 and the spatial
derivatives
and the spatial
derivatives 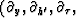
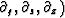 are associated
with
are associated
with 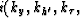 kg , ks , kz ).
Using these Fourier variables in the vectors of (66) and
differentiating
(58), (59), (60), and (61)
to find the indicated elements in the
matrix of (66), we get
kg , ks , kz ).
Using these Fourier variables in the vectors of (66) and
differentiating
(58), (59), (60), and (61)
to find the indicated elements in the
matrix of (66), we get
| ![\begin{displaymath}
\left[
\matrix {
\matrix { 1 \cr { - p } \cr p \cr { {2 \, ...
... { { - \omega' } \cr k_y \cr k_{{h}' } \cr k_{\tau} }
}
\right]\end{displaymath}](img135.gif) |
(67) |
Let S be the sine of the takeoff angle at the source and let G be
the sine of the emergent angle at the geophone.
If the velocity v is known, then these angles will be directly
measurable as stepouts on common-geophone gathers and common-shot gathers.
Likewise, on a constant-offset section or a slant stack, observed
stepouts relate to an apparent dip Y,
and on a linearly moved-out common-midpoint gather, stepouts
measure the apparent stepout H'.
The precise definitions are
|  |
(68) |
| (69) |
With these definitions the second and third rows of (67) become
| 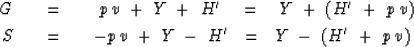 |
(70) |
| (71) |
The familiar offset stepout angle H is related to the
LMO residual stepout angle H' by H' = H -pv.
Setting H' equal to
zero means setting kh' equal to zero,
thereby indicating integration over h' , which in turn
indicates slant stacking data with slant angle p.
Small values of H' /v or 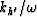 refer
to stepouts near to p.
refer
to stepouts near to p.





Next: Processing possibilities
Up: INTERVAL VELOCITY BY LINEAR
Previous: Common-midpoint Snell coordinates
Stanford Exploration Project
10/31/1997
![\begin{displaymath}
\left[ \
\matrix { \partial_t \cr \partial_g \cr \partial_s...
... \partial_y
\cr \partial_{{h}' } \cr \partial_{\tau} }
\right]\end{displaymath}](img128.gif)
![\begin{displaymath}
\left[ \
\matrix { \partial_t \cr \partial_g \cr \partial_s...
... \partial_y
\cr \partial_{{h}' } \cr \partial_{\tau} }
\right]\end{displaymath}](img128.gif)
![\begin{displaymath}
\left[
\matrix {
\matrix { 1 \cr { - p } \cr p \cr { {2 \, ...
... { { - \omega' } \cr k_y \cr k_{{h}' } \cr k_{\tau} }
}
\right]\end{displaymath}](img135.gif)
