




Next: Differential equations and Fourier
Up: INTERVAL VELOCITY BY LINEAR
Previous: Graphical method for interval
Common-midpoint slanted wave analysis is a more conservative approach to
seismic data analysis than the Snell wave approach.
The advantage of common-midpoint analysis is that the
effects of earth dip tend to show up mainly on the midpoint axis,
and the effect of seismic velocity shows up mainly on the offset axis.
Our immediate goal is to define an invertible, wave-equation approach
to determination of interval velocity.
The disadvantage of common-midpoint analysis is that it is nonphysical.
A slant stack at common geophone simulates a downgoing Snell wave,
and you expect to be able to write a differential equation to describe it,
no matter what ensues, be it multiple reflection or lateral velocity variation.
A common-midpoint slant stack does not model anything that is physically realizable.
Nothing says that a partial differential equation exists
to extrapolate such a stack.
This doesn't mean that there is necessarily anything wrong
with a common-midpoint
coordinate
system.
But it does make us respect the Snell wave approach even though
its use in the industrial world is not exactly growing by leaps and bounds.
(Someone implementing common-midpoint slant stack would immediately notice
that it is easier than slant stack on common-geophone data.
This is because at a common midpoint,
the tops of hyperboloids must be at zero offset,
the location of the Fresnel zone is more predictable,
and interpolation and missing data problems are much alleviated).
Seismic data is collected in time,
geophone, shot, and depth coordinates (t,g,s,z).
A new four-component system will now be defined.
Midpoint is defined in the usual way:
| 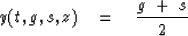 |
(51) |
Travel-time depth is defined using the vertical phase velocity in a borehole.
Two-way travel times are used,
in order to be as conventional as possible:
| 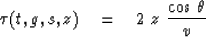 |
(52) |
Next the surface offset h' is defined.
We will not use the old definition of offset.
For this method, shots and geophones should not go straight down,
but along a ray.
This can be so if h' is defined as follows:
| 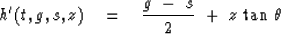 |
(53) |
With this new definition of h' the
separation of the shot and geophone decreases with depth
for constant h'.
Define the
LMO time
as the travel time in the point-source experiment less the linear moveout.
So, at any depth, the LMO time is 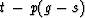 .As h' was defined to be the
surface
half-offset, t' is defined to be the
surface
LMO time.
From the LMO time of a buried experiment, the LMO time at the surface
is defined by adding in the travel-time depth of the experiment:
.As h' was defined to be the
surface
half-offset, t' is defined to be the
surface
LMO time.
From the LMO time of a buried experiment, the LMO time at the surface
is defined by adding in the travel-time depth of the experiment:
| 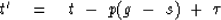 |
(54) |
You may like to think of (54) as a ``slant'' on time retardation
for upcoming waves, say, 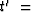
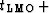
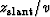 .Formally,
.Formally,
| 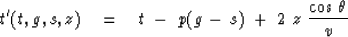 |
(55) |
Figure 17 is a geometrical representation of these concepts.
cmplmo
Figure 17
The CMP-LMO coordinate frame geometry.
This is a natural coordinate system for describing waves
that resemble a reference Snell wave.

From the geometry of Figure 17
it will be deduced that a measurement
of a reflection at some particular value of (h' ,t' ) directly
determines the velocity.
Write an equation for the reflector depth:
| 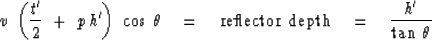 |
(56) |
Using Snell's law to eliminate angles and solving for velocity gives
| 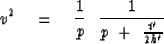 |
(57) |
This is consistent with equation (50).
Gathering the above definitions into a group,
and allowing for depth-variable
velocity by replacing z by the integral over z,
we get
| 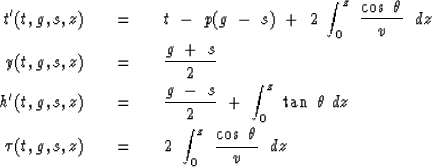 |
(58) |
| (59) |
| (60) |
| (61) |
Before these equations are used, all the
trigonometric functions must be eliminated by Snell's law for
stratified media, 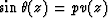 .Snell's parameter p is a numerical constant throughout the analysis.
.Snell's parameter p is a numerical constant throughout the analysis.
The equation for interval velocity determination (50) again
arises when dt' /dz from (58) and d h' /dz from (60)
are combined:
| 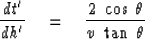 |
(62) |
Eliminating the trig functions with 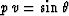 allows us
to solve for the interval velocity:
allows us
to solve for the interval velocity:
| 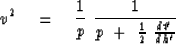 |
(63) |
At the earth's surface z= 0,
seismic survey data can be put into the coordinate frame
(58), (59), (60), and (61)
merely by making a numerical choice of p and doing the linear moveout.
No knowledge of velocity v(z) is required so far.
Then we look at the data for some tops of the skewed hyperbolas.
Finding some,
we use equation (50),
(57) or (63) to get a velocity
with which to begin downward continuation.
Waves can be described in either the (t,g,s,z) physical
coordinates or the newly defined coordinates 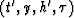 .In physical coordinates the image is found at
.In physical coordinates the image is found at
| 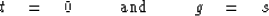 |
(64) |
To express these conditions in the Snell coordinates,
insert (64) into (58) and (61).
The result is what programmers call the
stopping condition:
| 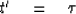 |
(65) |
This is the depth at which the velocity information should
be best focused in the ( h' ,t' )-plane.
Next some downward-continuation equations.





Next: Differential equations and Fourier
Up: INTERVAL VELOCITY BY LINEAR
Previous: Graphical method for interval
Stanford Exploration Project
10/31/1997
![]() .As h' was defined to be the
surface
half-offset, t' is defined to be the
surface
LMO time.
From the LMO time of a buried experiment, the LMO time at the surface
is defined by adding in the travel-time depth of the experiment:
.As h' was defined to be the
surface
half-offset, t' is defined to be the
surface
LMO time.
From the LMO time of a buried experiment, the LMO time at the surface
is defined by adding in the travel-time depth of the experiment:

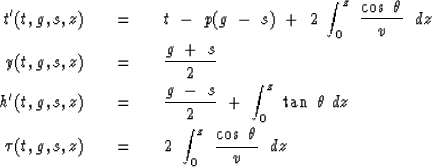
![]() .Snell's parameter p is a numerical constant throughout the analysis.
.Snell's parameter p is a numerical constant throughout the analysis.
![]() .In physical coordinates the image is found at
.In physical coordinates the image is found at