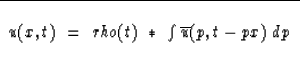Next: Plane-wave superposition
Up: SLANT STACK
Previous: Slant stack and Fourier
Tomography
in medical imaging is based on the same mathematics as
inverse slant stack.
Simply stated, (two-dimensional) tomography
or inverse slant stacking is the reconstruction
of a function given line integrals through it.
The inverse slant-stack formula will follow from the definition
of two-dimensional Fourier integration:
| ![\begin{displaymath}
u(x,t) \eq
\int\ e^{{-} i \omega t} \ [\ \int \ e^{{i} k x } \
U(k, \omega ) \ dk\ ]\ d \omega\end{displaymath}](img49.gif) |
(20) |
Substitute 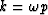 and
and 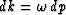 into (20).
Notice that when
into (20).
Notice that when 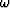 is negative the integration with dp runs from
positive to negative instead of the reverse.
To keep the integration in the conventional sense of negative to positive,
introduce the absolute value
is negative the integration with dp runs from
positive to negative instead of the reverse.
To keep the integration in the conventional sense of negative to positive,
introduce the absolute value 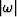 .(More generally, a change of variable of volume integrals introduces
the Jacobian of the transformation).
Thus,
.(More generally, a change of variable of volume integrals introduces
the Jacobian of the transformation).
Thus,
| ![\begin{eqnarray}
u(x,t)\ \ \ &=&\ \ \
\int\ e^{{-} i \omega t} \
[\ \int \ e^{...
...i} \omega p x } \
\vert \omega \vert \
] \
d \omega \ \ \
dp\\ end{eqnarray}](img52.gif) |
(21) |
| (22) |
Observe that the { } in (22) contain an inverse Fourier transform
of a product of three functions of frequency.
The product of three functions in the 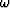 -domain is
a convolution in the time domain.
The three functions are first
-domain is
a convolution in the time domain.
The three functions are first 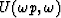 ,which by (19) is the FT of the slant stack.
Second is a delay operator
,which by (19) is the FT of the slant stack.
Second is a delay operator 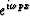 , i.e
an impulse function of time at time px.
Third is an
, i.e
an impulse function of time at time px.
Third is an 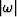 filter.
The
filter.
The 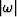 filter is called a rho filter.
The rho filter does not depend on p so we may separate it
from the integration over p.
Let ``*'' denote convolution.
Introduce the delay px as an argument shift.
Finally we have the inverse slant-stack equation we have been seeking:
filter is called a rho filter.
The rho filter does not depend on p so we may separate it
from the integration over p.
Let ``*'' denote convolution.
Introduce the delay px as an argument shift.
Finally we have the inverse slant-stack equation we have been seeking:
| 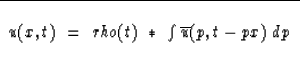 |
(23) |
It is curious that the inverse to the slant-stack operation (14)
is basically another slant-stacking operation (23) with a sign change.





Next: Plane-wave superposition
Up: SLANT STACK
Previous: Slant stack and Fourier
Stanford Exploration Project
10/31/1997
![\begin{eqnarray}
u(x,t)\ \ \ &=&\ \ \
\int\ e^{{-} i \omega t} \
[\ \int \ e^{...
...i} \omega p x } \
\vert \omega \vert \
] \
d \omega \ \ \
dp\\ end{eqnarray}](img52.gif)