




Next: Reflection coefficients spherical versus
Up: SLANT STACK
Previous: Inverse slant stack
Equation (23) can be simply interpreted
as plane-wave superposition.
To make this clear,
we first dispose of the rho filter by means of a definition.
| 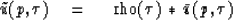 |
(24) |
Equation (24) will be seen to be more than a definition.
We will see that 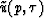 can be interpreted as the
plane-wave spectrum .
Substituting the definition (24)
into both (23) and (14) gives
another transform pair:
can be interpreted as the
plane-wave spectrum .
Substituting the definition (24)
into both (23) and (14) gives
another transform pair:
| 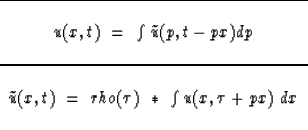 |
(25) |
To confirm that 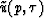 may be interpreted
as the plane-wave spectrum,
we take
may be interpreted
as the plane-wave spectrum,
we take 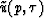 to be the impulse
function
to be the impulse
function 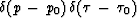 and
substitute it into the top half of (25).
The result
and
substitute it into the top half of (25).
The result 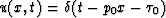 is an impulsive plane wave, as expected.
is an impulsive plane wave, as expected.





Next: Reflection coefficients spherical versus
Up: SLANT STACK
Previous: Inverse slant stack
Stanford Exploration Project
10/31/1997
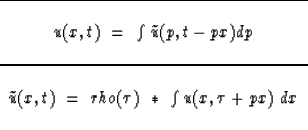
![]() may be interpreted
as the plane-wave spectrum,
we take
may be interpreted
as the plane-wave spectrum,
we take ![]() to be the impulse
function
to be the impulse
function ![]() and
substitute it into the top half of (25).
The result
and
substitute it into the top half of (25).
The result ![]() is an impulsive plane wave, as expected.
is an impulsive plane wave, as expected.