




Next: The xxz derivative
Up: FINITE DIFFERENCING
Previous: The Crank-Nicolson method
Much of the world's scientific computing power gets used up solving
tridiagonal simultaneous equations.
For reference and completeness the algorithm is included here.
Let the simultaneous equations be written as a difference
equation
| 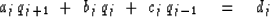 |
(39) |
Introduce new unknowns ej and fj,
along with an equation
| 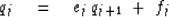 |
(40) |
Write (40) with shifted index:
| 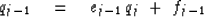 |
(41) |
Insert (41) into (39):
| 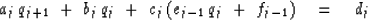 |
(42) |
Now rearrange (42) to resemble (15):
| 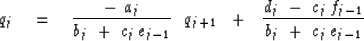 |
(43) |
Compare (43) to (40) to see recursions for
the new unknowns ej and fj:
| 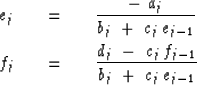 |
(44) |
| (45) |
First a boundary condition for the left-hand side must be given.
This may involve one or two points.
The most general possible end condition is a linear relation like
equation (40) at j=0, namely, 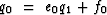 .Thus, the boundary condition must give us both e0 and f0.
With e0 and all the aj , bj , cj, we
can use (44) to compute all the ej.
.Thus, the boundary condition must give us both e0 and f0.
With e0 and all the aj , bj , cj, we
can use (44) to compute all the ej.
On the right-hand boundary we need a boundary condition.
The general two-point boundary condition is
| 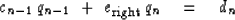 |
(46) |
Equation (46) includes as special cases the
zero-value and zero-slope boundary conditions.
Equation (46) can be compared to equation (41)
at its end.
| 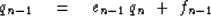 |
(47) |
Both qn and qn-1 are unknown,
but in equations (46) and (47) we have two equations,
so the solution is easy.
The final step is to take the value of qn and use it
in (41) to compute 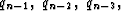 etc.
The subroutine rtris() solves
equation (38) for q where
n=5,
endl
etc.
The subroutine rtris() solves
equation (38) for q where
n=5,
endl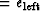 ,endr
,endr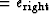 ,a=c
,a=c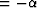 , and
b
, and
b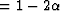 .
.
If you wish to squeeze every last ounce of power from your computer,
note some facts about this algorithm.
(1) The calculation of ej depends
on the medium through aj, bj, cj, but
it does not depend
on the
solution
qj (even through dj).
This means that it may be possible to save and reuse ej.
(2) In many computers, division is much slower than multiplication.
Thus, the divisor in (19a,b) can be inverted once
(and perhaps stored for reuse).





Next: The xxz derivative
Up: FINITE DIFFERENCING
Previous: The Crank-Nicolson method
Stanford Exploration Project
10/31/1997
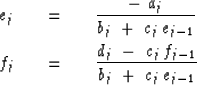
![]() .Thus, the boundary condition must give us both e0 and f0.
With e0 and all the aj , bj , cj, we
can use (44) to compute all the ej.
.Thus, the boundary condition must give us both e0 and f0.
With e0 and all the aj , bj , cj, we
can use (44) to compute all the ej.