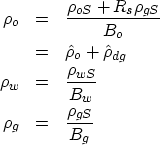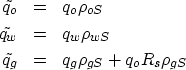Next: Implementation of a reservoir
Up: Wave propagation in an
Previous: Introduction
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) Unfortunately, a reservoir is difficult to access. It is buried
hundreds or thousands of meters in the subsurface.
A geoscientist only chance to access the reservoir directly
is in a well.
Petroleum engineers carefully observe a well's
production volumes of oil, water, and gas.
Additionally,
the engineers measure pressure in the well or
even conduct pressure tests.
My discussion of reservoir fluid flow processes follows
Landa 1997 and Aziz 1979.
Unfortunately, a reservoir is difficult to access. It is buried
hundreds or thousands of meters in the subsurface.
A geoscientist only chance to access the reservoir directly
is in a well.
Petroleum engineers carefully observe a well's
production volumes of oil, water, and gas.
Additionally,
the engineers measure pressure in the well or
even conduct pressure tests.
My discussion of reservoir fluid flow processes follows
Landa 1997 and Aziz 1979.
Black-oil model.
Petroleum engineers
use various reservoir fluid flow simulators to relate their
observations to reservoir properties, such as permeability,
porosity, pressure distribution, and saturation.
The standard black-oil model for a reservoirs mix of
fluids comprises
three distinct phases: oil, water, and gas.
The oil phase dissolves a certain amount of gas; the water does not.
Intuitively,
one might want to describe the reservoir properties at the scales of pores.
However, the traditional approach homogenizes the pore-scale heterogenities
to macroscopic descriptions such as Darcy's law.
The general equation of mass conservation
| 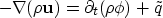 |
(1) |
asserts that any local change in the flow of mass
is due to a local source (or sink) 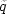 or a temporal change
in density or porosity.
The source
or a temporal change
in density or porosity.
The source 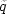 is a location's local well production which
is zero for any location without a producing well.
The vector
is a location's local well production which
is zero for any location without a producing well.
The vector 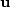 is the fluid flux, and
is the fluid flux, and 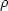 is the fluid density.
is the fluid density.
Darcy's law
expresses the fluid flux in terms of pressure and gravity
| 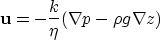 |
(2) |
where
k is the permeability, and
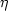 is the viscosity.
The second term on the right hand side incorporates the gravitational
effect, where g is the gravitational acceleration.
Darcy's law is only valid for slow flow rates, where turbulence and
inertia are negligible.
Darcy's law 2
generalizes to the flow of multiple phases - oil, water, gas -
in a porous rock:
is the viscosity.
The second term on the right hand side incorporates the gravitational
effect, where g is the gravitational acceleration.
Darcy's law is only valid for slow flow rates, where turbulence and
inertia are negligible.
Darcy's law 2
generalizes to the flow of multiple phases - oil, water, gas -
in a porous rock:
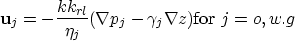
where krl is the relative permeability of each phase.
The relative permeability is a function of saturation.
Aziz 1979 discusses various empirical expressions
for that dependency.
The combination of Darcy's law with
the mass conservation equation 1
yields the fluid flow equations:
| ![\begin{eqnarray}
\nabla [\gamma_o (\nabla p_o - \rho_o g \nabla z)] &=&
\partia...
...\frac{R_s S_o}{B_o} \frac{S_g}{B_g}] + R_s q_o + q_{fg}.
\nonumber\end{eqnarray}](img8.gif) |
|
| (3) |
| |
The equations relate differences in pressure gradient - left hand side -
to temporal changes in pore saturation - right hand side.
The equations are complemented by three additional constraints
| 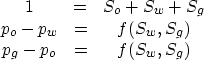 |
(4) |
The first equation states that the rock is saturated by the three
fluids. The two bottom equations relate capillary pressures and
saturations and are usually empiric Aziz and Settari (1979).
The parameters Bj relate parameter values at surface conditions
- indicated by index S - and
reservoir condition - indicated by index R.
The parameters are defined as volume ratio
| ![\begin{displaymath}
\begin{array}
{ccccc}
B_o &=& \frac{[V_o]_R + [V_{dg}]_R}{[V...
...p_w) \\ B_g &=& \frac{[V_g]_R} {[V_g]_S} &=& f(p_g) \end{array}\end{displaymath}](img10.gif) |
(5) |
and are based on the pressure-volume-temperature (PVT) constant
at thermodynamic equilibrium.
The first equation deviates from the other two since it accounts for
the dissolved gas volume Vdg.
The volume ratios Bj let us relate the density at reservoir conditions
to the density at surface conditions:
| 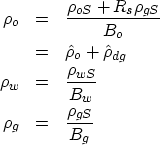 |
|
| (6) |
| |
| |
The mass transfer between the oil and gas phase is defined as
Rs = [Vdg / Vo]S.
The Bj ratios, and the mass transfer Rs,
depend on the pressure pj of the
various phases j=o,w,g.
Since water compressibility is small, the relationship
Bw = f(pw) can be approximated by
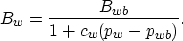
The analogue expressions for Bo, Bg, Rs, and 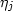 are empiric and again discussed by Aziz and Settari (1979).
are empiric and again discussed by Aziz and Settari (1979).
The coefficients 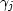 in equation 4
express transmissibilities and are defined as
in equation 4
express transmissibilities and are defined as
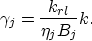
Viscosities 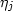 of oil and gas strongly depend on temperature
and pressure. The pressure dependency is again empirical Aziz and Settari (1979).
The viscosity's temperature dependence
is especially important in thermal-recovery
processes such as steam injections.
In general, the temperature dependency is well approximated by
of oil and gas strongly depend on temperature
and pressure. The pressure dependency is again empirical Aziz and Settari (1979).
The viscosity's temperature dependence
is especially important in thermal-recovery
processes such as steam injections.
In general, the temperature dependency is well approximated by
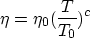
where 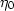 and T0 are reference points and c
is a fluid specific constant.
and T0 are reference points and c
is a fluid specific constant.
Finally, porosity is often pressure dependent
![\begin{displaymath}
\phi = \phi_0 \exp(c_R(p - p_0)) \approx \phi_0 [1 + c_R(p - p_0)]\end{displaymath}](img18.gif)
where cR is the bulk compressibility of the rock and the porosity 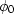 and
and 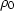 refer to known reference values.
refer to known reference values.
The equations
| 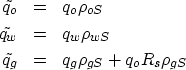 |
|
| (7) |
| |
relate the in situ volumes 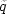 of equation 1
to the production volumes q
as they appear at the well head under standard surface condition.
of equation 1
to the production volumes q
as they appear at the well head under standard surface condition.
Well observations.
In a field experiment,
petroleum engineers control the pressure in the well.
Petroleum engineers conduct well tests by changing the pressure in the
well and observing the reaction of the surrounding reservoir pressure
(respectively its effect on the controlled well pressure).
These experiments attempt to estimate local reservoir transmissibility
but do have to account for the skin effect:
the alterations of the rock next to the well.
Additionally,
petroleum engineers record the well's production volumes.
The production volumes depend on the reservoir pressure p and the
well bore pressure pwf:
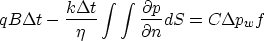
where
q the volume production rate per unit of time at the surface
(not at reservoir pressure),
B is the formation volume factor,
C represents the ability of the well bore to store fluids,
n is the normal of the well bore,
S the well bore's surface.
I hope to combine such well observations with seismic time-lapse
data to yield improved estimates of reservoir property maps.
Simplified well system
My preliminary implementation is based on the assumption
that the reservoir only contains a single fluid,
e.g. oil but neither water, nor gas.
This assumption might be locally reasonable for large oil fields,
albeit I expect almost all hydrocarbon mixtures to release gas when
a production lowers the reservoir pressure sufficiently.
The assumption of a single
fluid phase collapses the fluid flow equations 4 and its
constraints 4 to a single equation.
Additionally, I neglect gravitational forces (g =0).
I assume that the rocks transmissibility 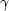 varies smoothly
and that the rocks pore volume is independent of pressure (cR = 0).
Finally, I suggest that the reservoir fluid is only slightly
compressible and consequently satisfies
varies smoothly
and that the rocks pore volume is independent of pressure (cR = 0).
Finally, I suggest that the reservoir fluid is only slightly
compressible and consequently satisfies
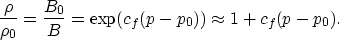
Under these assumption the equation system for multiple phases
collapses to the diffusivity equation
| 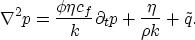 |
(8) |
This single phase fluid flow equation for porous rocks
can be derived directly
from the corresponding versions of Darcy's law and the
mass conservation Raghavan (1993).
I doubt that seismic field data can detect reasonable changes
in pressure and density of a single fluid phase around a well.
Instead, current time lapse surveys concentrate on detecting saturation
changes in multi-phase reservoirs, that often involve gas, steam,
or highly pressured water.
I chose the single fluid phase case
since it is the simplest to implement.
Should I continue this work, I will seek the collaboration of an
experienced petroleum engineer to improve the reservoir flow
simulator.
The simplicity of the reservoir model, however,
might prove beneficial when formulating the inverse problem.
Parameterization
My simple reservoir simulator requires as input
a transmissibility map of the reservoir,
an initial pressure distribution within the reservoir
(usually assumed to be constant),
the pressure history at the boundary of the wells.
Given these parameters, the simulator computes
the reservoir pressure distribution over time.
For this preliminary study,
I restrict the reservoir to a two-dimensional plane.
The model is computationally manageable, and the results
can be visualized effectively.





Next: Implementation of a reservoir
Up: Wave propagation in an
Previous: Introduction
Stanford Exploration Project
3/9/1999
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) Unfortunately, a reservoir is difficult to access. It is buried
hundreds or thousands of meters in the subsurface.
A geoscientist only chance to access the reservoir directly
is in a well.
Petroleum engineers carefully observe a well's
production volumes of oil, water, and gas.
Additionally,
the engineers measure pressure in the well or
even conduct pressure tests.
My discussion of reservoir fluid flow processes follows
Landa 1997 and Aziz 1979.
Unfortunately, a reservoir is difficult to access. It is buried
hundreds or thousands of meters in the subsurface.
A geoscientist only chance to access the reservoir directly
is in a well.
Petroleum engineers carefully observe a well's
production volumes of oil, water, and gas.
Additionally,
the engineers measure pressure in the well or
even conduct pressure tests.
My discussion of reservoir fluid flow processes follows
Landa 1997 and Aziz 1979.
![\begin{eqnarray}
\nabla [\gamma_o (\nabla p_o - \rho_o g \nabla z)] &=&
\partia...
...\frac{R_s S_o}{B_o} \frac{S_g}{B_g}] + R_s q_o + q_{fg}.
\nonumber\end{eqnarray}](img8.gif)
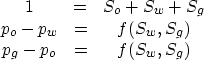
![\begin{displaymath}
\begin{array}
{ccccc}
B_o &=& \frac{[V_o]_R + [V_{dg}]_R}{[V...
...p_w) \\ B_g &=& \frac{[V_g]_R} {[V_g]_S} &=& f(p_g) \end{array}\end{displaymath}](img10.gif)