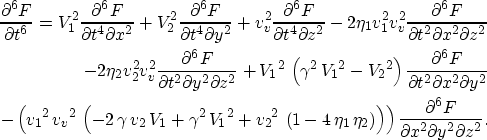Next: About this document ...
Up: Alkhalifah: Wave equation for
Previous: REFERENCES
In the text we derived an acoustic dispersion relation [equation 17] for orthorhombic anisotropy.
This relation can be used to derive the acoustic wave equation following the same steps I took
in deriving such an equation for VTI media Alkhalifah (1997b).
First, we cast the dispersion relation in a polynomial form in terms of the slownesses and
substitute these slownesses with wavenumbers as follows,
| 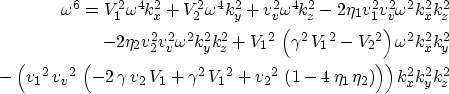 |
|
| |
| (27) |
where 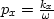 ,
, 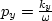 , and
, and 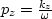 .As a reminder, V1 and V2 are the horizontal velocities along the x-axis and
the y-axis, respectively.
Multiplying both sides of equation (27) by the wavefield
in the Fourier domain,
.As a reminder, V1 and V2 are the horizontal velocities along the x-axis and
the y-axis, respectively.
Multiplying both sides of equation (27) by the wavefield
in the Fourier domain, 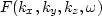 ,as well as using inverse Fourier transform on kx, ky, and kz
(
,as well as using inverse Fourier transform on kx, ky, and kz
(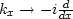 ,
, 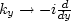 , and
, and
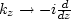 ) yields a wave equation in the space-frequency domain,
given by
) yields a wave equation in the space-frequency domain,
given by
| 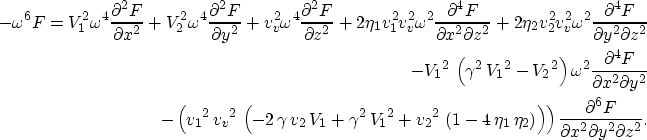 |
|
| |
| (28) |
Finally, applying inverse Fourier transform on  (
(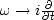 ),
the acoustic wave equation for
VTI media is given by
),
the acoustic wave equation for
VTI media is given by
| 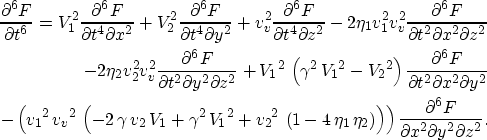 |
|
| |
| (29) |
Unlike the acoustic wave equation for
VTI media Alkhalifah (1997b) which is fourth order in time,
equation (29) is sixth order in time, and thus can provide us with
6 independent solutions.





Next: About this document ...
Up: Alkhalifah: Wave equation for
Previous: REFERENCES
Stanford Exploration Project
8/21/1998
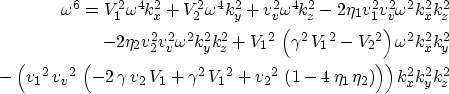
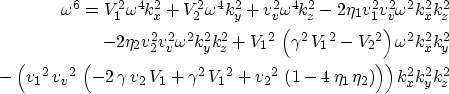
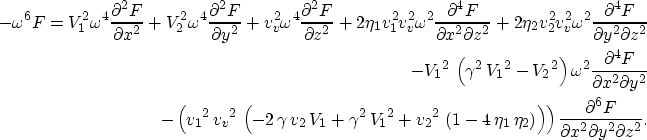
![]() (
(![]() ),
the acoustic wave equation for
VTI media is given by
),
the acoustic wave equation for
VTI media is given by