In this section, We will look at three anisotropic models given by ![]() equal 0.1, 0.2 and 0.3.
Though, stronger anisotropy may exist, the majority of anisotropy in the subsurface
conveniently lies within this range.
equal 0.1, 0.2 and 0.3.
Though, stronger anisotropy may exist, the majority of anisotropy in the subsurface
conveniently lies within this range.
Figure 4 shows AMO operators for the first example,
which is a homogeneous VTI medium with ![]() .
.
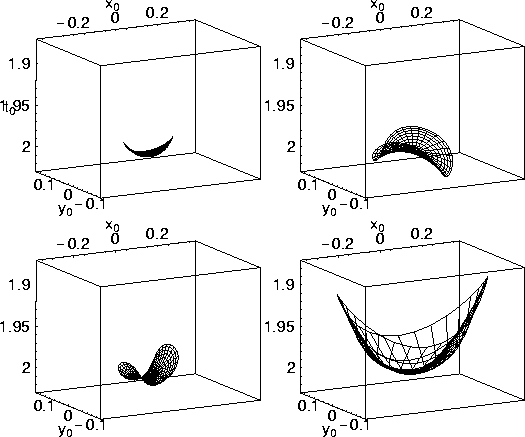 |
The AMO operator corresponding to a pure offset correction, shown upper left, has a similar shape to the full 3-D DMO operator, shown lower-right, both concaved upward. The corresponding residual DMO operator for isotropic media is a purely 2-D operator. The azimuth-correction-only operator, shown upper right, differs from the isotropic-medium one shown in Figure 1. When the offset and azimuth corrections are combined in a single operator, it is given by the one shown in the lower left of Figure 4. The full DMO operator, shown in the lower-right, is clearly the largest in size. AMO operators that include offset correction alters the position of horizontal, as well as dipping, reflections. This alteration is necessary to correct for the non-hyperbolic moveout associated with VTI media for horizontal and dipping events.
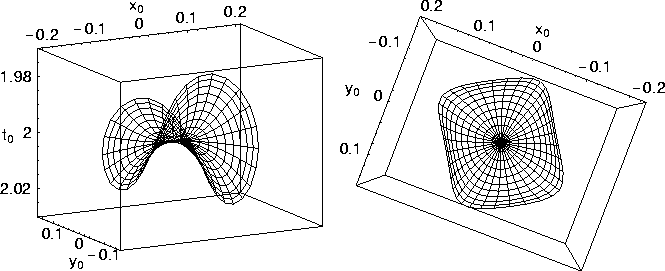 |
Figure 5 shows a side and a top view of the AMO operator (shown in
Figure 4 upper-right corner) that corrects for
an azimuth of 30 degrees. The homogeneous medium has a v=2 km/s and ![]() =0.1.
The anisotropic AMO operator is clearly a stretched version of the isotropic one, shown in
Figure 1. A similar stretch behavior
exists in DMO operators in anisotropic media Alkhalifah (1997c). In addition, the presence of anisotropy has altered the shape
of the AMO operator. This is more evident on the top view, where the circular shape of the isotropic
AMO operator is becoming more rectangular in anisotropic media. These changes in the AMO operator due to anisotropy is clearly larger than the
ones associated with smooth (linear in this case)
vertical velocity variation (Figure 2). Thus, anisotropy can pause a bigger problem
to the conventional AMO than vertical velocity variation.
=0.1.
The anisotropic AMO operator is clearly a stretched version of the isotropic one, shown in
Figure 1. A similar stretch behavior
exists in DMO operators in anisotropic media Alkhalifah (1997c). In addition, the presence of anisotropy has altered the shape
of the AMO operator. This is more evident on the top view, where the circular shape of the isotropic
AMO operator is becoming more rectangular in anisotropic media. These changes in the AMO operator due to anisotropy is clearly larger than the
ones associated with smooth (linear in this case)
vertical velocity variation (Figure 2). Thus, anisotropy can pause a bigger problem
to the conventional AMO than vertical velocity variation.
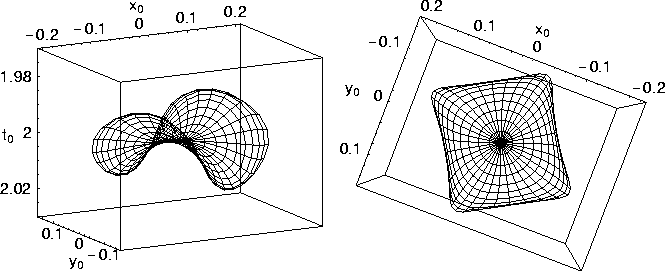 |
A stronger anisotropy (Figure 6), with ![]() =0.2, causes the AMO operator to stretch
even more. It also results in triplications that takes place at moderate dip angles. A closer look, given by
the inline and crossline components of the AMO operator (Figure 7),
reveals such triplications in detail. These triplications
exist in both the inline and crossline components of the AMO operator, as well as, all angles in between.
=0.2, causes the AMO operator to stretch
even more. It also results in triplications that takes place at moderate dip angles. A closer look, given by
the inline and crossline components of the AMO operator (Figure 7),
reveals such triplications in detail. These triplications
exist in both the inline and crossline components of the AMO operator, as well as, all angles in between.
 |
Figure 8 shows AMO operators for an even stronger anisotropy with ![]() , and same velocity
used previously.
, and same velocity
used previously.
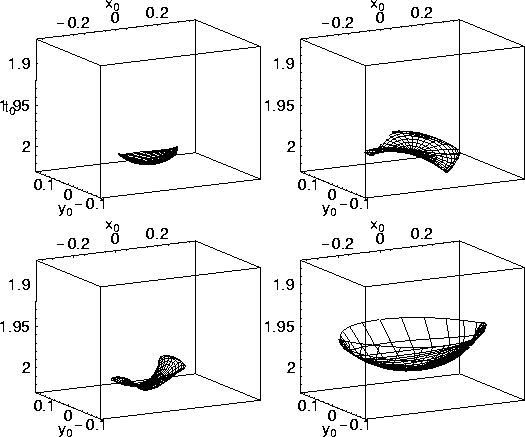 |
The AMO operator corresponding to a pure offset correction,
shown upper left, again has a similar shape to the
full 3-D DMO operator, shown lower-right, which is generally concaved upward.
The crossline component of this operator is mainly the result of anisotropy.
Recall that the corresponding residual DMO operator
for isotropic media is a purely 2-D operator. The size of this out-of-plane component is greater for this
strong anisotropy model than that
for ![]() =0.1 (Figure 4 upper-left corner), and therefore the size of the crossline component is
dependent on the strength of anisotropy. The same observation holds for DMO operators, shown lower-right
corners of Figures 4 and 8.
The azimuth-correction-only operator, shown upper right, differs considerably
from the isotropic-medium
one shown in Figure 1.
When the offset and azimuth corrections
are combined in a single operator,
it is given by the one shown in the lower
left of Figure 8, and it is simply given by the convolution of the offset operator (upper-left)
and the azimuth operator (upper-right).
=0.1 (Figure 4 upper-left corner), and therefore the size of the crossline component is
dependent on the strength of anisotropy. The same observation holds for DMO operators, shown lower-right
corners of Figures 4 and 8.
The azimuth-correction-only operator, shown upper right, differs considerably
from the isotropic-medium
one shown in Figure 1.
When the offset and azimuth corrections
are combined in a single operator,
it is given by the one shown in the lower
left of Figure 8, and it is simply given by the convolution of the offset operator (upper-left)
and the azimuth operator (upper-right).
Figure 9 shows a side and a top view of the AMO operator (shown in
Figure 8 upper-right corner) that corrects for
an azimuth of 30 degrees. The homogeneous medium has v=2 km/s and ![]() =0.3.
=0.3.
 |
Again, the same conclusions hold here with regard to the impact of anisotropy on the AMO operator, which is obviously stronger than the impact of the smooth vertical velocity variation, given by Figure 2. Clearly, this operator is very different from the isotropic one; the anisotropic operator is stretched and has a more rectangular shape.