Azimuth moveout correction in isotropic media

Azimuth moveout correction relies heavily on shape of the operator used in the application. Since these operators are convolved with the data their shapes and sizes may significantly influence the output of the operation. The time shift to be applied to the data is a function of the difference vector ${\bf \Delta m}=\Delta m(\cos \Delta \varphi,\sin \Delta \varphi)$ between the midpoint of the input trace and the midpoint of the output trace. The impulse response of the AMO operator in isotropic media has a general skewed saddle shape. In fact, for homogeneous isotropic media, the shape of the saddle is given by the following analytical equation  

$${t}_{2}\left({{\bf \Delta m}},{{\bf h}_{1}},{{\bf h}_{2}},{t... ...\theta_1-\theta_2)-\Delta m^2\sin^2(\theta_1-\Delta \varphi)}},$$ (1)

where the offset vector of the input data is ${\bf h}_{1}=h_{1}\cos\theta_{1}{\bf x}+h_{1}\sin\theta_{1}{\bf y}=h_{1}(\cos\theta_{1},\sin\theta_{1})$and the offset vector of the desired output data is ${\bf h}_{2}=h_{2}(\cos \theta_{2},\sin \theta_{2})$.The unit vectors $\bf x$ and $\bf y$ point respectively in the in-line direction and the cross-line direction, respectively. The traveltimes t₁ and t₂ are respectively the traveltime of the input data after NMO has been applied, and the traveltime of the results before inverse NMO has been applied.

 

AMO2eta0
Figure 1 A side (left) and a top (right) view of the AMO operator for an isotropic homogeneous medium with an input and output offset of 2 km and correction to only the azimuth of 30 degrees. The x₀ (inline) and y₀ (crossline) axes are in km and the t₀ is in seconds. This holds here and throughout. The circular lines are contours of equal ray parameter.

Figure 1 shows a side and a top view of the 30-degrees correction AMO operator for an isotropic homogeneous medium. It is clearly 3-D in structure and has a general skewed saddle shape. The saddle is altered 30 degrees from the inline direction, in agreement with the amount of azimuth correction applied. The AMO operator domain has an overall circular shape. The shape of this AMO domain appears to be different from the one presented by Biondi et al. (1998) (a parallelogram), because I limit the zero-offset ray parameters when plotting the AMO operator.

Alkhalifah and Biondi (1998) generated AMO operators for isotropic v(z) media. They used a nifty approach to build their AMO operators for v(z) media. A similar approach is used here, but discussed below, to build the anisotropic AMO operators.

 

AMO2vzeta0
Figure 2 A side (left) and a top (right) view of the AMO operator for a linear v(z) medium for an input and output offset of 2 km and correction to only the azimuth of 30 degrees. The linear velocity increase with depth is given by v(z)=1.5+0.6 z km/s, which gives a root-mean-squared velocity of about 2 km/s at the input NMO corrected time of 2 s.

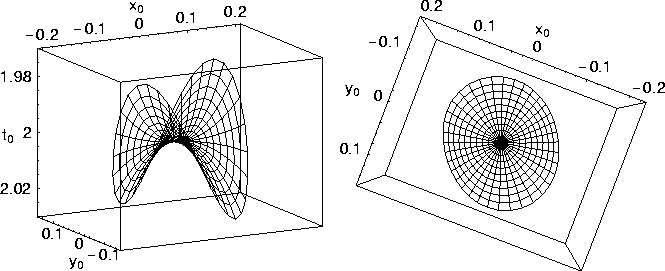Figure 2 shows a side and a top view of the 30-degrees correction AMO operator for a v(z) medium, in which velocity increase with depth linearly as v(z)=1.5+0.6 z km/s, where z is the depth given in km. Again, the saddle is altered 30 degrees from the inline direction, in agreement with the amount of azimuth correction applied. The root-mean-square (rms) velocity for this model is similar to the homogeneous one and is equal to 2 km/s. Clearly, the v(z) operator is very similar in shape and size to the homogeneous one, shown in Figure 1. Thus, Alkhalifah and Biondi (1998) concluded that the influence smooth velocity variations on the AMO operator is small.