Setting x-x0=0 in the offset-midpoint traveltime equation yields a formula that describes the moveout of reflections from horizontal reflectors. Since many of these moveout equations exist Hake et al. (1984); Tsvankin and Thomsen (1994), I will compare the offset axis of our VTI offset-midpoint traveltime equation with these equations, as well as with the exact solution computed numerically. Specifically, I will measure the difference in traveltimes between the various moveout approximations and the numerically computed solution. This difference is given in terms of the percentage error in traveltime as a function of offset. Clearly all approximations yield the exact solution for zero-offset, since they are derived based on this limit.
For a horizontal reflector x-x0=0, as well as px=0, in equations (12) and (13), and thus they reduce to
| |
(17) |
![]()
Hake et al. (1984) derived a three-term Taylor series expansion for the moveout of reflections
from horizontal interfaces in homogeneous, VTI media. Their traveltime
equation can be simplified when expressed in terms of ![]() and v Alkhalifah and Tsvankin (1995), as follows:
and v Alkhalifah and Tsvankin (1995), as follows:
| |
(18) |
Tsvankin and Thomsen (1994) derived a correction factor to the nonhyperbolic term of Hake et al's 1984
equation that increases the accuracy and stabilizes traveltime moveout at large offsets in VTI media.
The more accurate moveout equation, when expressed in terms of ![]() and v
Alkhalifah and Tsvankin (1995), and slightly
manipulated, is given by
and v
Alkhalifah and Tsvankin (1995), and slightly
manipulated, is given by
| |
(19) |
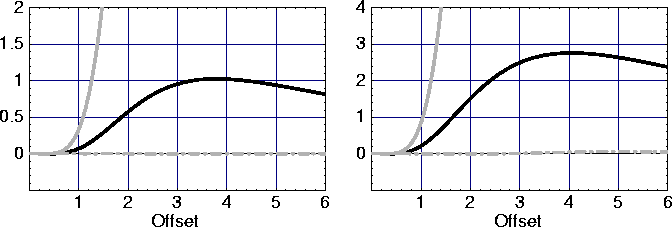 |
Figure 3 shows the percentage error in traveltime moveout as a function of offset for the three
moveout equations given above. Clearly, the offset-axis component of the new VTI pyramid equation
(dashed gray curve) has less errors and is
by far more accurate than the traveltime moveout given by
either the three-term Taylors series equation (18)
(solid gray curve) or the modified traveltime moveout equation (19) (solid black curve).
In fact, the errors in equation (17) for moderate anisotropy, given by
![]() (left), and relatively strong anisotropy, given by
(left), and relatively strong anisotropy, given by ![]() (right),
are practically zero for offsets-to-depth ratio up to 3, shown here.
(right),
are practically zero for offsets-to-depth ratio up to 3, shown here.
|
Erroreta1
Figure 4 Same as Figure 3, but with | 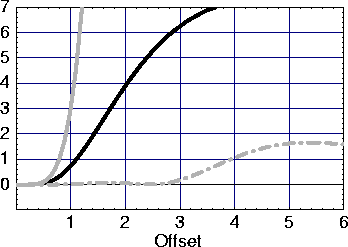 |
We have to use a model with ![]() equals the huge value of 1, as
shown in Figure 4, before observing any sizable errors in
the new equation. Even for such a huge anisotropy, the errors are again practically zero
for offsets-to-depth ratio
below 1.5. Therefore, for all intent and
purposes in seismic applications, equation (8) for horizontal reflectors is practically exact.
Next, we test the accuracy of the midpoint-offset pyramid equation for dipping reflectors. We do that
by prestack migrating synthetic data that include dipping reflections using this new equation.
equals the huge value of 1, as
shown in Figure 4, before observing any sizable errors in
the new equation. Even for such a huge anisotropy, the errors are again practically zero
for offsets-to-depth ratio
below 1.5. Therefore, for all intent and
purposes in seismic applications, equation (8) for horizontal reflectors is practically exact.
Next, we test the accuracy of the midpoint-offset pyramid equation for dipping reflectors. We do that
by prestack migrating synthetic data that include dipping reflections using this new equation.