Cheop's pyramid for VTI media

To find the maximum of equation (8), we take its derivative with respect to p_h and p_x, and set these derivatives to zero. The stationary point along the p_h-p_x plane is obtained by solving the two new nonlinear equations in terms of p_x and p_h. Since the source rayparameter, p_s, and the receiver rayparameter, p_g, are linearly related to p_x and p_h, as follows

p_s = p_x - p_h,

and

p_g = p_x + p_h,

we can find the stationary point solution by solving for p_s and p_g, instead of solving for p_x and p_h. Solving for p_s and p_g yields two independent nonlinear equations corresponding to the source and receiver rays, that can be solved separately.

The stationary point solutions (Appendix A) are then given by  

$$p^2 =\frac{{y^2}\,\left( {y^6} + 6\,{v^2}\,{y^4}\,\left( 1... ...\eta \right) \,{{\tau }^4} + 4\,{v^6}\,{{\tau }^6} \right) },$$ (9)

where y is either the lateral distance between the image point and source, given by 2(x-x₀-h) for p_s, or the lateral distance between the image point and receiver, given by 2(x-x₀+h) for p_g.

For isotropic media, $\eta=0$ and equation (9) reduces to  

$$p_{\rm is}^2 =\frac{{y^2}}{{v^2}\,{y^2} + {v^4}\,{{\tau }^2}},$$ (10)

where

$$\sin^2\theta = \frac{{y^2}}{{y^2} + {v^2}\,{{\tau }^2}},$$ (11)

and

$$p_{\rm is} = \frac{\sin\theta}{v}.$$

As a result,  

$$p^2 = p_{\rm is}^2 \,\,\frac{\left( {y^6} + 6\,{v^2}\,{y^4... ...,\eta \right) \,{{\tau }^4} + 4\,{v^6}\,{{\tau }^6} \right)},$$ (12)

For traveltime calculation, equation (9) for p_s and p_g is inserted into  

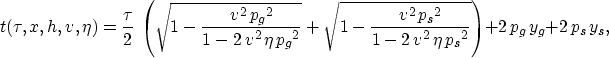$$t(\tau,x,h,v,\eta) = {\frac{\tau}{2} \,\left( {\sqrt{1 - {... ...\,{{{p_s}}^2}}}}} \right) } + 2\,{p_g}\,y_g + 2\,{p_s}\,y_s,$$ (13)

where y_s =2(h - x + x₀) and y_g=2(h + x - x₀).

Equation (13) is the offset-midpoint (Cheop's pyramid) equation for VTI media. The derivation included the stationary phase (high frequency) approximation, as well as approximations corresponding to small $\eta$. For $\eta$=0, equation (13) reduces to the exact form (high-frequency limit) for isotropic media. However, for large $\eta$the equation, as we will see later, is extremely accurate.

 

pyr3
Figure 2 Traveltime, in seconds, as a function offset, X, and midpoint, x, both in km, for, from left to right, an isotropic media ($\eta=0$), a VTI media with $\eta=0.2$, and a VTI media with $\eta=0.4$, respectively. The velocity is 2 km/s and the vertical time is 1 s, for all three pyramids.

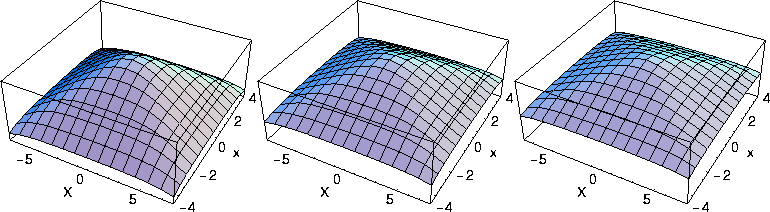Figure 2 shows the traveltime calculated using equation (13) as a function of offset and midpoint for three $\eta$ values. The shape of the traveltime function resembles Cheop's pyramid, and as a result was given the name. Unlike the isotropic medium pyramid, the VTI ones include nonhyperbolic moveout along the offset and midpoint axis. Clearly, the higher horizontal velocity in the VTI media resulted in faster traveltime with increasing offset and midpoint than the isotropic case.

The stationary phase method also provides an amplitude factor given by the second derivative of the phase function [equation (8)] with respect to p_s and p_g. Specifically, the amplitude is proportional to the reciprocal of the square root of the second derivative of the phase evaluated at the stationary point (Appendix C).