




Next: Vertically heterogenous media
Up: Rickett, et al.: STANFORD
Previous: REFERENCES
To evaluate the integrals in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), using the stationary phase method, we need to calculate
the maximum of the phase function, which for VTI media is given by
), using the stationary phase method, we need to calculate
the maximum of the phase function, which for VTI media is given by
| 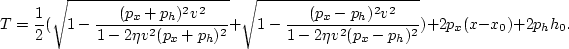 |
(136) |
Since the relation between the source-receiver rayparameters (ps and pg) and the offset-midpoint
rayparameters (ph and px) is linear, we can evaluate the stationary points by solving for
ps and pg instead of ph and px,
| 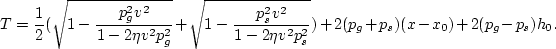 |
(137) |
Setting the derivative of equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in terms of ps and pg to
zero provides us with two independent equations that can be solved for ps and pg,
separately. Physically, this implies that we are solving
for the source-to-image-point traveltime and receiver-to-image-point traveltime, separately,
which makes complete sense.
The ps and pg stationary point solutions can be used later to evaluate ph and px.
in terms of ps and pg to
zero provides us with two independent equations that can be solved for ps and pg,
separately. Physically, this implies that we are solving
for the source-to-image-point traveltime and receiver-to-image-point traveltime, separately,
which makes complete sense.
The ps and pg stationary point solutions can be used later to evaluate ph and px.
First, ps is evaluated by solving
| 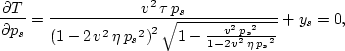 |
(138) |
where ys=2(x-x0-h0). Similarly, pg is evaluated by solving
| 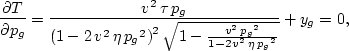 |
(139) |
where yg=2(x-x0+h0). Equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is similar to equation
is similar to equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , with ys replaced by yg, and
ps replaced by pg. Therefore, solving for ps will yield an equation that can be used to
solve for pg as well.
, with ys replaced by yg, and
ps replaced by pg. Therefore, solving for ps will yield an equation that can be used to
solve for pg as well.
To remove the square root in equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I move ys to the other side of the
equation and square both sides. This will allow us to right equation
, I move ys to the other side of the
equation and square both sides. This will allow us to right equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in a polynomial form as follows,
in a polynomial form as follows,
| 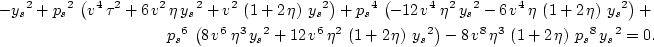 |
|
| (140) |
This is a fourth-order polynomial in ps2, which can be solved exactly for the four roots in ps2.
However, these four roots are given by highly complicated equations which include square roots as
well as powers of the order 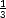 . Such equations are not useful for practical use.
Thus, I elect to use Shanks transform to obtain approximations that are almost exact, yet more useful
for practical implementations. Also, since Shanks transform is based on perturbation theory, it will provide us
with the desired solution of ps2 among the four possible solutions;
the solution based on perturbation from an isotropic model.
. Such equations are not useful for practical use.
Thus, I elect to use Shanks transform to obtain approximations that are almost exact, yet more useful
for practical implementations. Also, since Shanks transform is based on perturbation theory, it will provide us
with the desired solution of ps2 among the four possible solutions;
the solution based on perturbation from an isotropic model.
Using Shanks transform, described in Appendix D, we obtain
| 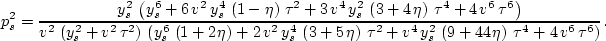 |
(141) |
Again, pg is given by the same equation but with ys replaced by yg.
B





Next: Vertically heterogenous media
Up: Rickett, et al.: STANFORD
Previous: REFERENCES
Stanford Exploration Project
7/5/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), using the stationary phase method, we need to calculate
the maximum of the phase function, which for VTI media is given by
), using the stationary phase method, we need to calculate
the maximum of the phase function, which for VTI media is given by
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in terms of ps and pg to
zero provides us with two independent equations that can be solved for ps and pg,
separately. Physically, this implies that we are solving
for the source-to-image-point traveltime and receiver-to-image-point traveltime, separately,
which makes complete sense.
The ps and pg stationary point solutions can be used later to evaluate ph and px.
in terms of ps and pg to
zero provides us with two independent equations that can be solved for ps and pg,
separately. Physically, this implies that we are solving
for the source-to-image-point traveltime and receiver-to-image-point traveltime, separately,
which makes complete sense.
The ps and pg stationary point solutions can be used later to evaluate ph and px.
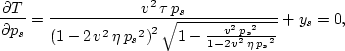
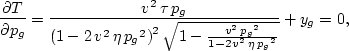
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is similar to equation
is similar to equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , with ys replaced by yg, and
ps replaced by pg. Therefore, solving for ps will yield an equation that can be used to
solve for pg as well.
, with ys replaced by yg, and
ps replaced by pg. Therefore, solving for ps will yield an equation that can be used to
solve for pg as well.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I move ys to the other side of the
equation and square both sides. This will allow us to right equation
, I move ys to the other side of the
equation and square both sides. This will allow us to right equation ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) in a polynomial form as follows,
in a polynomial form as follows,