




Next: Cheop's pyramid for VTI
Up: The midpoint-offset traveltime equation
Previous: The midpoint-offset traveltime equation
The Phase-shift operator in a prestack Fourier-domain is described
by the double-square-root equation, which is a function of the angular frequency  ,the midpoint rayparameter px, the offset rayparameter ph, and the velocity, v.
Constant-velocity prestack migration, with output provided in two-way vertical time (
,the midpoint rayparameter px, the offset rayparameter ph, and the velocity, v.
Constant-velocity prestack migration, with output provided in two-way vertical time ( ),
in offset-midpoint coordinates (), is given by:
),
in offset-midpoint coordinates (), is given by:
| 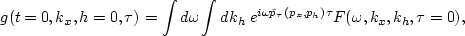 |
(119) |
where 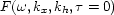 is the 3-D Fourier transform
of the field
is the 3-D Fourier transform
of the field 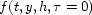 recorded at the surface, given by
recorded at the surface, given by
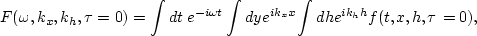
and 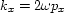 ,
, 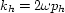 , and
, and 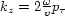 are
the horizontal midpoint wavenumber, the horizontal offset wavenumber, and the vertical
wavenumber, respectively.
In this paper, I will freely alternate between the half offset, h, and the full offset, X, in
representing the offset axis,
where X=2h. The phase factor
are
the horizontal midpoint wavenumber, the horizontal offset wavenumber, and the vertical
wavenumber, respectively.
In this paper, I will freely alternate between the half offset, h, and the full offset, X, in
representing the offset axis,
where X=2h. The phase factor 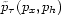 , for isotropic media, is defined as
, for isotropic media, is defined as
| ![\begin{displaymath}
{\tilde{p}_{\tau}(p_x,p_h)} \equiv
{ \frac{1}{2} (\left[1 -
...
...{1 \over 2}
+\left[1 -
v^2 (p_x-p_h)^2\right]^{1 \over 2}) },\end{displaymath}](img369.gif) |
(120) |
which is a normalized version of the double-square-root (DSR) equation.
The two integrals in  and kh in equation (
and kh in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
represent the imaging
condition for zero offset and zero time (h=0,t=0).
)
represent the imaging
condition for zero offset and zero time (h=0,t=0).
For VTI media, the phase factor is given by a more complicated equation (),
| 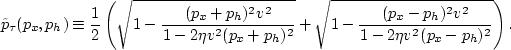 |
(121) |
The dispersion equation, now, includes  as well as the velocity.
as well as the velocity.
Kirchhoff migration is typically applied by smearing an input trace, after the proper traveltime
shifts, over the output section in a summation process. To obtain the response of inserting
a single trace into the prestack phase-shift migration [equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )], we multiply the input data by a Direc-delta
function in midpoint and offset axes as follows
)], we multiply the input data by a Direc-delta
function in midpoint and offset axes as follows
| 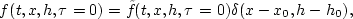 |
(122) |
where x0 is the midpoint location and h0 is the offset of the input trace.
The Fourier transform of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is given by
) is given by
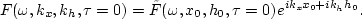
Inserting this equation into equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) provides us with the migration response
to a single input trace given by
) provides us with the migration response
to a single input trace given by
| 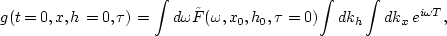 |
(123) |
where the new phase shift function is given by
| 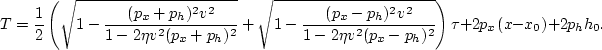 |
(124) |
The number of integrals in Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be reduced by recognizing areas in the integrand that contribute
the most to the integrals in kh and kx.
Since the integrand is an oscillatory function its biggest contributions
take place when the oscillations are stationary, when the phase function is either
minimum or maximum. This approach is referred to as the stationary phase method (Appendix C). The stationary
points (px and ph) correspond to
the minimum or maximum of equation (
) can be reduced by recognizing areas in the integrand that contribute
the most to the integrals in kh and kx.
Since the integrand is an oscillatory function its biggest contributions
take place when the oscillations are stationary, when the phase function is either
minimum or maximum. This approach is referred to as the stationary phase method (Appendix C). The stationary
points (px and ph) correspond to
the minimum or maximum of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In fact, the phase has
a dome-like shape as a function of px and ph (see Figure
). In fact, the phase has
a dome-like shape as a function of px and ph (see Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Thus, to calculate the stationary
points, we must set the derivative of equation (
). Thus, to calculate the stationary
points, we must set the derivative of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with respect to ph and
px to zero, and solve the two equations for these two parameters. An easier approach is discussed next and
in Appendix A.
) with respect to ph and
px to zero, and solve the two equations for these two parameters. An easier approach is discussed next and
in Appendix A.
station
Figure 1 Traveltime, in seconds, as a function offset-midpoint rayparameters (left),
and source-receiver rayparameters (right) computed using equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). All rayparameters have units of s/km.
In both plots, the midpoint shift x-x0=0.1 km, the offset is 0.2 km, and vertical time of 1 s. The
medium parameters considered are v=2 km/s,
). All rayparameters have units of s/km.
In both plots, the midpoint shift x-x0=0.1 km, the offset is 0.2 km, and vertical time of 1 s. The
medium parameters considered are v=2 km/s, 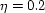 .
.






Next: Cheop's pyramid for VTI
Up: The midpoint-offset traveltime equation
Previous: The midpoint-offset traveltime equation
Stanford Exploration Project
7/5/1998
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
represent the imaging
condition for zero offset and zero time (h=0,t=0).
)
represent the imaging
condition for zero offset and zero time (h=0,t=0).
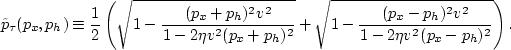
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )], we multiply the input data by a Direc-delta
function in midpoint and offset axes as follows
)], we multiply the input data by a Direc-delta
function in midpoint and offset axes as follows
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is given by
) is given by
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) provides us with the migration response
to a single input trace given by
) provides us with the migration response
to a single input trace given by
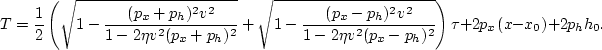
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be reduced by recognizing areas in the integrand that contribute
the most to the integrals in kh and kx.
Since the integrand is an oscillatory function its biggest contributions
take place when the oscillations are stationary, when the phase function is either
minimum or maximum. This approach is referred to as the stationary phase method (Appendix C). The stationary
points (px and ph) correspond to
the minimum or maximum of equation (
) can be reduced by recognizing areas in the integrand that contribute
the most to the integrals in kh and kx.
Since the integrand is an oscillatory function its biggest contributions
take place when the oscillations are stationary, when the phase function is either
minimum or maximum. This approach is referred to as the stationary phase method (Appendix C). The stationary
points (px and ph) correspond to
the minimum or maximum of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In fact, the phase has
a dome-like shape as a function of px and ph (see Figure
). In fact, the phase has
a dome-like shape as a function of px and ph (see Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Thus, to calculate the stationary
points, we must set the derivative of equation (
). Thus, to calculate the stationary
points, we must set the derivative of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with respect to ph and
px to zero, and solve the two equations for these two parameters. An easier approach is discussed next and
in Appendix A.
) with respect to ph and
px to zero, and solve the two equations for these two parameters. An easier approach is discussed next and
in Appendix A.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). All rayparameters have units of s/km.
In both plots, the midpoint shift x-x0=0.1 km, the offset is 0.2 km, and vertical time of 1 s. The
medium parameters considered are v=2 km/s,
). All rayparameters have units of s/km.
In both plots, the midpoint shift x-x0=0.1 km, the offset is 0.2 km, and vertical time of 1 s. The
medium parameters considered are v=2 km/s,