




Next: Cross-spectral factorization
Up: Rickett, et al.: 3D
Previous: The 45 wave equation
The helix transform Claerbout (1997) provides boundary
conditions that map multi-dimensional convolution into
one-dimension. In this case, the 2-D convolution
operator, 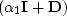 , can be recast as
an equivalent 1-D filter.
, can be recast as
an equivalent 1-D filter.
Helical boundary conditions allow the two-dimensional convolution
matrix, 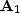 , to be expressed as a one-dimensional
convolution with a filter of length 2 Nx +1 that has the form
, to be expressed as a one-dimensional
convolution with a filter of length 2 Nx +1 that has the form
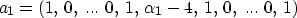
The structure of the finite-difference Laplacian operator, 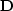 ,
is simplified when compared to equation (9).
,
is simplified when compared to equation (9).
| ![\begin{displaymath}
{\bf D} = \left[
\begin{array}
{cccccccc}
& & & & & & & \\ ...
...& & & & \\ . & . & . & 1 & . & . & 1 & -4 \\ \end{array}\right]\end{displaymath}](img29.gif) |
(10) |
The 1-D filter can be factored into a causal and anti-causal
parts, and the matrix inverse can be computed by recursive polynomial
division (1-D deconvolution).





Next: Cross-spectral factorization
Up: Rickett, et al.: 3D
Previous: The 45 wave equation
Stanford Exploration Project
7/5/1998
![]() , to be expressed as a one-dimensional
convolution with a filter of length 2 Nx +1 that has the form
, to be expressed as a one-dimensional
convolution with a filter of length 2 Nx +1 that has the form
![]()
![\begin{displaymath}
{\bf D} = \left[
\begin{array}
{cccccccc}
& & & & & & & \\ ...
...& & & & \\ . & . & . & 1 & . & . & 1 & -4 \\ \end{array}\right]\end{displaymath}](img29.gif)