




Next: Helical boundary conditions
Up: Implicit extrapolation
Previous: Implicit extrapolation
The diffraction term of the in the 45 equation Claerbout (1985) can
be rewritten as the following matrix equation, by inserting the rational
part of the implicit extrapolator (3) into
equation (1):
equation Claerbout (1985) can
be rewritten as the following matrix equation, by inserting the rational
part of the implicit extrapolator (3) into
equation (1):
| 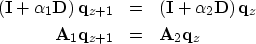 |
(5) |
| (6) |
where the complex coefficients 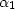 and
and 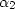 can be
calculated, and
can be
calculated, and 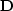 is a finite-difference representation of the
Laplacian,
is a finite-difference representation of the
Laplacian, 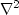 .
.
The right-hand-side of equation (6) is known. The
challenge is to find the vector 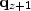 by inverting the
matrix,
by inverting the
matrix, 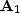 .Given the wavefield on the surface, this equation provides a way to
downward-continue in depth.
.Given the wavefield on the surface, this equation provides a way to
downward-continue in depth.
The matrices in equation (6) represent convolution with
a scaled finite-difference Laplacian, with its main diagonal stabilized.
Scaling coefficients, 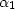 and
and 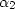 , are complex and
depend on the ratio,
, are complex and
depend on the ratio, 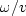 .
.
In the two-dimensional problem, the 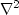 operator acts only in
the x-direction, and can be represented by the three-point
convolutional filter, d=(1,-2,1). The matrix,
operator acts only in
the x-direction, and can be represented by the three-point
convolutional filter, d=(1,-2,1). The matrix, 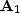 ,therefore, has a tridiagonal structure, which can be inverted
efficiently with a recursive solver.
,therefore, has a tridiagonal structure, which can be inverted
efficiently with a recursive solver.
In three-dimensional wavefield extrapolation, the 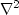 operator
acts in both the x and y-directions.
operator
acts in both the x and y-directions.
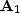 and
and 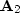 therefore represent 2-D convolution, and
d can be represented by the a simple 5-point filter,
therefore represent 2-D convolution, and
d can be represented by the a simple 5-point filter,
| ![\begin{displaymath}
d = \left[ \begin{array}
{ccc}
& 1 & \\ 1 & -4 & 1\\ & 1 & \end{array} \right] \end{displaymath}](img21.gif) |
(7) |
or a more isotropic 9-point filter Iserles (1996),
| ![\begin{displaymath}
d = \left[ \begin{array}
{ccc}
1/6 & 2/3 & 1/6 \\ 2/3 & -10/3 & 2/3\\ 1/6 & 2/3 & 1/6\end{array} \right]\end{displaymath}](img22.gif) |
(8) |
The vectors 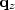 and
and 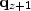 contain the wavefield at
every point in the (x,y)-plane.
Therefore, the convolution matrices that operate on
them are square with dimensions
contain the wavefield at
every point in the (x,y)-plane.
Therefore, the convolution matrices that operate on
them are square with dimensions 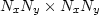 .
As an illustration, for a
.
As an illustration, for a 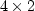 spatial plane, the structure of
matrix
spatial plane, the structure of
matrix 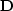 with the five-point approximation and transient
boundary conditions, will be the blocked-tridiagonal matrix
with the five-point approximation and transient
boundary conditions, will be the blocked-tridiagonal matrix
| ![\begin{displaymath}
{\bf D} = \left[
\begin{array}
{cccc\vert cccc}
-4 & 1 & . ...
... & & & \\ . & . & . & 1 & . & . & 1 & -4 \\ \end{array}\right]\end{displaymath}](img26.gif) |
(9) |
This blocked system cannot be easily
inverted, even for the case of constant velocity, since the missing
coefficients on the second diagonals break the Toeplitz structure.





Next: Helical boundary conditions
Up: Implicit extrapolation
Previous: Implicit extrapolation
Stanford Exploration Project
7/5/1998
![]() by inverting the
matrix,
by inverting the
matrix, ![]() .Given the wavefield on the surface, this equation provides a way to
downward-continue in depth.
.Given the wavefield on the surface, this equation provides a way to
downward-continue in depth.
![]() and
and ![]() , are complex and
depend on the ratio,
, are complex and
depend on the ratio, ![]() .
.![]() operator acts only in
the x-direction, and can be represented by the three-point
convolutional filter, d=(1,-2,1). The matrix,
operator acts only in
the x-direction, and can be represented by the three-point
convolutional filter, d=(1,-2,1). The matrix, ![]() ,therefore, has a tridiagonal structure, which can be inverted
efficiently with a recursive solver.
,therefore, has a tridiagonal structure, which can be inverted
efficiently with a recursive solver.
![]() operator
acts in both the x and y-directions.
operator
acts in both the x and y-directions.
![]() and
and ![]() therefore represent 2-D convolution, and
d can be represented by the a simple 5-point filter,
therefore represent 2-D convolution, and
d can be represented by the a simple 5-point filter,
![\begin{displaymath}
d = \left[ \begin{array}
{ccc}
& 1 & \\ 1 & -4 & 1\\ & 1 & \end{array} \right] \end{displaymath}](img21.gif)
![\begin{displaymath}
d = \left[ \begin{array}
{ccc}
1/6 & 2/3 & 1/6 \\ 2/3 & -10/3 & 2/3\\ 1/6 & 2/3 & 1/6\end{array} \right]\end{displaymath}](img22.gif)
![\begin{displaymath}
{\bf D} = \left[
\begin{array}
{cccc\vert cccc}
-4 & 1 & . ...
... & & & \\ . & . & . & 1 & . & . & 1 & -4 \\ \end{array}\right]\end{displaymath}](img26.gif)