




Next: The amplitude transport equation
Up: VTI processing in inhomogeneous
Previous: REFERENCES
In this appendix, we derive  , given by equation 6, in the
, given by equation 6, in the
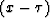 -domain. Using such an equation can avoid the process of mapping
-domain. Using such an equation can avoid the process of mapping  from
depth to time and back.
The vertical two-way traveltime,
from
depth to time and back.
The vertical two-way traveltime,  , is written as
, is written as
| 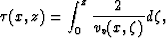 |
(29) |
where z corresponds to depth.
Similarly,
| 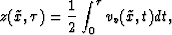 |
(30) |
where 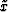 corresponds to the new coordinate system.
corresponds to the new coordinate system.
Using the chain rule,
| 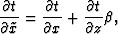 |
(31) |
where 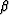 extracted from equation (30) is given by
extracted from equation (30) is given by
| 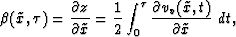 |
(32) |
the partial derivative in  is
is
| 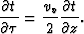 |
(33) |
Therefore, the
transformation from (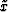 ,
,  ) to (x, z) is governed
by the following Jacobian matrix in 2-D:
) to (x, z) is governed
by the following Jacobian matrix in 2-D:
| 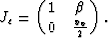 |
(34) |
The inverse of Jc is
| 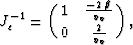 |
(35) |
which should equal the Jacobian matrix for the transformation from (x, z) to (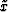 ,
,  ),
given by
),
given by
| 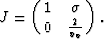 |
(36) |
As a result,
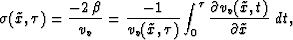
which is a convenient equation,
since we want to keep all fields, including velocity, in 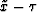 coordinates.
coordinates.
B





Next: The amplitude transport equation
Up: VTI processing in inhomogeneous
Previous: REFERENCES
Stanford Exploration Project
10/9/1997
![]() , given by equation 6, in the
, given by equation 6, in the
![]() -domain. Using such an equation can avoid the process of mapping
-domain. Using such an equation can avoid the process of mapping ![]() from
depth to time and back.
The vertical two-way traveltime,
from
depth to time and back.
The vertical two-way traveltime, ![]() , is written as
, is written as
![]()