




Next: raytracing equations
Up: VTI processing in inhomogeneous
Previous: The depth issue
In this section, we derive the relation between the depth and vertical time axis
for a general inhomogeneous
medium. Using this relation, the VTI eikonal equation is represented in the new 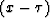 -domain
coordinate system. We have derived a similar relation in another
paper Biondo et al. (1997); for
isotropic media. Also Hatton et al. (1981) implemented a similar mapping to show the limitations
of time migration.
-domain
coordinate system. We have derived a similar relation in another
paper Biondo et al. (1997); for
isotropic media. Also Hatton et al. (1981) implemented a similar mapping to show the limitations
of time migration.
Two-way vertical time is related to depth by the following relation,
| 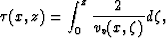 |
(3) |
where vv is the vertical P-wave velocity, which can vary vertically as well as laterally.
As follows from equation 3, the stretch applied to the depth axis is laterally variant.
Alkhalifah (1997b) derived a simple form of the eikonal equation for VTI media, based on setting
the shear wave velocity to zero. For 2-D media, it is
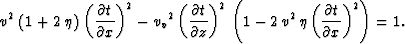
This equation, based on the acoustic medium assumption in VTI media,
though not physically possible, yields extremely
accurate traveltime solutions that are close to what we get for
typical elastic media.
The eikonal equation includes first-order derivatives of traveltime with respect
to position. In order to transform this eikonal equation from the
depth to the time coordinate, we need to replace x with 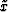 .Using the chain rule,
.Using the chain rule, 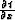 in the eikonal equation 4
is given by
in the eikonal equation 4
is given by
| 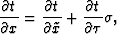 |
(5) |
where  , extracted from equation (3), is written as
, extracted from equation (3), is written as
| 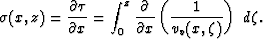 |
(6) |
Likewise, the partial derivative in z in the eikonal equation is
| 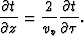 |
(7) |
Therefore, the
transformation from (x, z) to (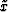 ,
,  ) is governed
by the following Jacobian matrix in 2-D media:
) is governed
by the following Jacobian matrix in 2-D media:
| 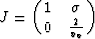 |
(8) |
Substituting equations (5) and (7)
into the eikonal equation (4) yields the equation
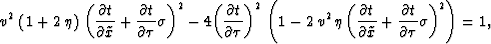
which is indirectly independent of the vertical velocity. However,
according to equation (6),  still depends on the vertical P-wave velocity. Rewriting
equation (6) in terms of the two-way
vertical time (see Appendix A) gives us
still depends on the vertical P-wave velocity. Rewriting
equation (6) in terms of the two-way
vertical time (see Appendix A) gives us
| 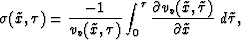 |
(10) |
where 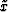 corresponds to the new coordinates (
corresponds to the new coordinates (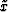 ,
,  ). In the case
of
). In the case
of 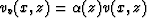 ,
which is a special case of lateral inhomogeneity,
referred to here as laterally factorized,
equation (6) takes the form
,
which is a special case of lateral inhomogeneity,
referred to here as laterally factorized,
equation (6) takes the form
| 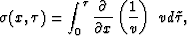 |
(11) |
which is clearly independent of the vertical P-wave velocity. Also,
equation (10) becomes
| 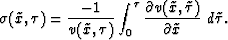 |
(12) |
The eikonal equation
can be used
to compute seismic traveltimes in laterally factorized inhomogeneous media without the need to estimate
the vertical P-wave velocity. The departure of the medium from this special
condition of laterally factorized media
will cause errors in traveltime
calculation. We can estimate these errors by evaluating how much  varies between equations (6)
and (11). Specifically, if
varies between equations (6)
and (11). Specifically, if 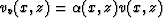 then
then
| 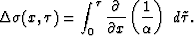 |
(13) |
If the ratio of the vertical to NMO velocity,  , does not change laterally,
, does not change laterally,
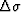 is equal to zero, and thus no errors will occur in traveltime calculation.
The departure of
is equal to zero, and thus no errors will occur in traveltime calculation.
The departure of  from zero affects only the x axis component of the wavefront;
according
to equations (5) and (7) it is
only
from zero affects only the x axis component of the wavefront;
according
to equations (5) and (7) it is
only 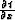 that depends on
that depends on  .
The vertical component of the traveltime remains accurate no matter
how much
.
The vertical component of the traveltime remains accurate no matter
how much  varies laterally. Also, because the eikonal equation is independent of
varies laterally. Also, because the eikonal equation is independent of
 for vertically traveling waves (
for vertically traveling waves (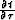 =0), such
waves are error-free. The majority of the errors caused by lateral
=0), such
waves are error-free. The majority of the errors caused by lateral  variation
occurs around 45-degree wave propagation.
variation
occurs around 45-degree wave propagation.
In terms of VTI parameters, the NMO velocity is given by Thomsen (1986)
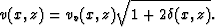
Therefore,
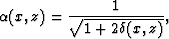
and
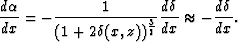
Then
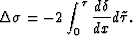
We can see that the absolute error, resulting from the integral formulation, clearly increases with time.
In addition, when we use the new coordinate
system 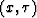 , the transport equation becomes independent of
the vertical velocity under the same condition of laterally factorized media (see Appendix B).
Bellow, and
for simplicity, we will
replace
, the transport equation becomes independent of
the vertical velocity under the same condition of laterally factorized media (see Appendix B).
Bellow, and
for simplicity, we will
replace 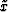 with x to denote the lateral coordinate in the new coordinate system.
with x to denote the lateral coordinate in the new coordinate system.





Next: raytracing equations
Up: VTI processing in inhomogeneous
Previous: The depth issue
Stanford Exploration Project
10/9/1997
![]() -domain
coordinate system. We have derived a similar relation in another
paper Biondo et al. (1997); for
isotropic media. Also Hatton et al. (1981) implemented a similar mapping to show the limitations
of time migration.
-domain
coordinate system. We have derived a similar relation in another
paper Biondo et al. (1997); for
isotropic media. Also Hatton et al. (1981) implemented a similar mapping to show the limitations
of time migration.
![]() .Using the chain rule,
.Using the chain rule, ![]() in the eikonal equation 4
is given by
in the eikonal equation 4
is given by
![]() still depends on the vertical P-wave velocity. Rewriting
equation (6) in terms of the two-way
vertical time (see Appendix A) gives us
still depends on the vertical P-wave velocity. Rewriting
equation (6) in terms of the two-way
vertical time (see Appendix A) gives us
![]()
![]()
![]()
![]()
![]() , the transport equation becomes independent of
the vertical velocity under the same condition of laterally factorized media (see Appendix B).
Bellow, and
for simplicity, we will
replace
, the transport equation becomes independent of
the vertical velocity under the same condition of laterally factorized media (see Appendix B).
Bellow, and
for simplicity, we will
replace ![]() with x to denote the lateral coordinate in the new coordinate system.
with x to denote the lateral coordinate in the new coordinate system.