Whether an AGC window or a more careful geometric spreading correction has been applied, two generations of seismic survey will, in general, have different time-varying gain functions applied to them. If not compensated for correctly, this may lead to a systematic leakage of non-reservoir events into the difference section. Although an amplitude correction may need to be time and space-varying, it should be constrained to vary very slowly, so it is not influenced by changes in the reservoir zone.
The simplest approach to amplitude balancing is to scale the data
based on the r.m.s. energy in the two surveys. However, this assumes
that the energy present in the noise fields are the same in both
datasets, or of much smaller magnitude than the signal energy.
Following a similar model to that used to describe the
failings of matched-filtering we can consider the two normalized
datasets, ![]() and
and ![]() , to consist of some shared
signal,
, to consist of some shared
signal, ![]() , and uncorrelated ``noise'' components,
, and uncorrelated ``noise'' components,
![]() and
and ![]() , which include the reservoir difference
anomaly we seek:
, which include the reservoir difference
anomaly we seek:
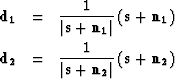
In order to rescale the signals to the same level, we need to apply a
scale factor, ![]() to
to ![]() , such that
, such that
| (8) |
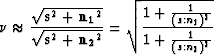 |
(9) |
The value of ![]() applied to
applied to ![]() has a large effect on
the amplitude of coherent events in the difference section, and
consequently may significantly affect the interpretation of the 4D
data. Unfortunately, the value of
has a large effect on
the amplitude of coherent events in the difference section, and
consequently may significantly affect the interpretation of the 4D
data. Unfortunately, the value of ![]() cannot be obtained directly
from the data without an a priori assumption about the nature of
the noise. Also the optimum value of
cannot be obtained directly
from the data without an a priori assumption about the nature of
the noise. Also the optimum value of ![]() may be time and space
varying, which further complicates its determination.
may be time and space
varying, which further complicates its determination.
Fortunately, for seismic data with high signal-to-noise
(![]() ), the equal energy (
), the equal energy (![]() ) balancing will
be valid since
) balancing will
be valid since ![]() will be very small.
will be very small.
| (10) |
In the past we have been estimating a value for ![]() by eye
from difference sections by sweeping through a range of scalar values and
finding one that minimizes the non-reservoir coherent energy in the
difference sections. This is unsatisfactory in that it can be overly
subjective. However an alternative approach is to make
a priori estimations of the signal-to-noise ratio's, and use
Equation 9 to calculate
by eye
from difference sections by sweeping through a range of scalar values and
finding one that minimizes the non-reservoir coherent energy in the
difference sections. This is unsatisfactory in that it can be overly
subjective. However an alternative approach is to make
a priori estimations of the signal-to-noise ratio's, and use
Equation 9 to calculate ![]() .
.
For the synthetic example described below, three
independent ``eyeball'' estimates of ![]() were 0.77, 0.81 and 0.80.
Knowing the noise fields exactly, the value obtained with the formula
above was 0.808.
were 0.77, 0.81 and 0.80.
Knowing the noise fields exactly, the value obtained with the formula
above was 0.808.
In production environments we expect to use an F-X decon method to estimate noise levels present in the two surveys. Alternatively, the amplitude of a marker horizon above the reservoir could be used to scale the datasets to the correct level.