![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)




Next: Focusing eikonal equation
Up: Table of Contents
``Focusing'' eikonal equation and global tomography
Biondo Biondi, Sergey Fomel, and Tariq Alkhalifah
biondo@sep.stanford.edu, sergey@sep.stanford.edu, tariq@sep.stanford.edu
ABSTRACT
The transformation of the eikonal equation from depth
coordinates (z,x)
into vertical-traveltime coordinates (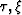 )enables the computation of reflections traveltimes
independent of depth-mapping.
This separation allows
the focusing and mapping
steps to be performed sequentially
even in the presence of complex velocity functions,
that otherwise would ``require'' depth migration. )enables the computation of reflections traveltimes
independent of depth-mapping.
This separation allows
the focusing and mapping
steps to be performed sequentially
even in the presence of complex velocity functions,
that otherwise would ``require'' depth migration.
The traveltimes satisfying the transformed eikonal equation
can be numerically evaluated by solving the associated
ray tracing equations.
The application of Fermat's principle
leads to the expression of linear relationships
between perturbations in traveltimes and
perturbations in focusing velocity.
This linearization, in conjunction with ray tracing,
can be used for a tomographic estimation
of focusing velocity.
|
Velocity has a dual role in reflection-seismic imaging.
It is needed
to focus the data through migration,
and to map the reflectors in depth
by converting arrival times into depths.
These two imaging goals are often conflicting.
The velocity function that best focuses the data
is not necessarily the velocity that performs the
correct depth mapping.
The focusing velocity is the velocity that best
predicts the relative delays between
reflections originated at the same point in the subsurface
and recorded at different offsets and midpoints.
We can measure these relative delays and
try to estimate the focusing velocity by
solving an inverse problem.
On the contrary, the mapping velocity
mostly affects the absolute delays of the reflections.
If we do not know the depth of the reflectors,
we cannot estimate the mapping velocity from reflection data.
To estimate mapping velocity we need other source of information,
such as well data and a priori geological information.
This distinction between focusing and mapping velocity
is routinely used when the data it time imaged,
and is one of the source of robustness of the time-imaging procedure.
In time imaging, the data are first focused by
determining stacking and/or RMS velocities,
then map-migrated to depth along
the image rays using an appropriate mapping velocity
Hubral (1977); Larner et al. (1981).
Unfortunately this useful separation is lost when
the data are imaged using depth migration.
In this case the same velocity field is used
to focus the data and to map the reflectors.
The main reason for this shortcoming of depth migration
is not conceptual, but it is imposed by limitations
in current depth-migration algorithms.
In this paper we present a method for computing
migration operators for Kirchhoff-like migrations
as a function of the focusing velocity.
The method is based on
a coordinate transformation
from depth to two-way vertical traveltime
applied to the eikonal equation.
We demonstrate that under fairly mild assumptions
on the relation between focusing and mapping velocities,
the traveltimes computed using the transformed eikonal
are only functions of the focusing velocity.
As a result, we call the transformed eikonal equation
the focusing eikonal.
The focusing eikonal has potential applications
to the estimation of focusing velocities.
It enables us to apply to depth-migration problems
the same sequential estimation of the two
interval velocities that is possible in time imaging.
One problem with the joint estimation
of the two velocities is that
a velocity perturbation not only causes changes in
the focusing of the data but it also causes
a vertical shift of both the reflectors and velocity
that are below the perturbation.
These vertical shifts present a challenge
to reflection tomography,
and are one of the reasons why layer-stripping procedures
are considered to be more robust than global tomographic procedures.
However, because global tomography has the potential to be more accurate
than layer stripping,
there are many incentives to stabilizing
global tomography.
We propose to perform the whole velocity estimation
in the vertical traveltime domain.
When the velocity function and the reflector geometry
are expressed in the vertical-traveltime coordinates,
their position is only weakly dependent on velocity.
Therefore, we may ameliorate the problems associated
with inaccuracies in the mapping velocity.
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)




Next: Focusing eikonal equation
Up: Table of Contents
Stanford Exploration Project
10/10/1997
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)