To analyze the linearity of the forward modeling, we compare the linearization errors of the two different tomographic methods. We define the linearization errors as the differences between the reflection traveltimes modeled with the true model, and the reflection traveltimes that are predicted by linearizing the forward modeling at the starting model. To compute the traveltimes perturbations we set as velocity perturbations the difference between the true model and the starting model.
The true model for the first example
is a positive Gaussian-shaped velocity anomaly
with peak amplitude of 0.5 km/s
superimposed onto a constant velocity background
of 2 km/s.
We positioned two flat reflectors.
The deep reflector at 3 km is below the anomaly,
while the shallow one at 2 km cuts through the anomaly.
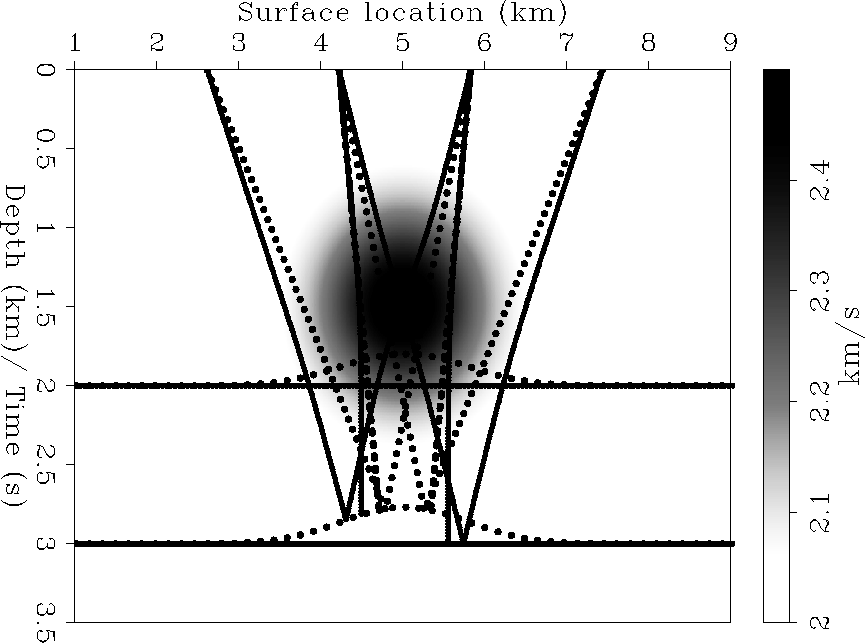
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the true velocity model with
superimposed both the starting (dashed lines)
and the true reflectors (solid lines)
along with few reflected raypaths.
The raypaths on the left are traced in the
shows the true velocity model with
superimposed both the starting (dashed lines)
and the true reflectors (solid lines)
along with few reflected raypaths.
The raypaths on the left are traced in the ![]() domain
while the raypaths on the right are traced in the
domain
while the raypaths on the right are traced in the ![]() domain.
We can notice how both the reflectors
and the rays move less in the
domain.
We can notice how both the reflectors
and the rays move less in the ![]() representation.
representation.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows comparison of the linearization errors in modeling
traveltimes of the reflections from the deeper reflector.
The errors are shown as a function of the midpoint
for two different offsets.
The thicker lines show the errors at zero offset,
and the thinner lines show the errors at 3.2 km offset.
The solid lines show the error in the
shows comparison of the linearization errors in modeling
traveltimes of the reflections from the deeper reflector.
The errors are shown as a function of the midpoint
for two different offsets.
The thicker lines show the errors at zero offset,
and the thinner lines show the errors at 3.2 km offset.
The solid lines show the error in the ![]() domain
and the dashed lines show the errors in
domain
and the dashed lines show the errors in ![]() domain.
There is no significant differences in errors
between the two domains.
This result is not surprising since the background model is constant
and the deeper reflector does not interfere with the anomaly.
domain.
There is no significant differences in errors
between the two domains.
This result is not surprising since the background model is constant
and the deeper reflector does not interfere with the anomaly.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows comparison of the linearization errors in modeling
traveltimes of the reflections from the shallower reflector.
In this case the reflector interferes with the anomaly,
and the errors for
shows comparison of the linearization errors in modeling
traveltimes of the reflections from the shallower reflector.
In this case the reflector interferes with the anomaly,
and the errors for ![]() domain tomography are smaller.
We explain these differences with the interference
between the reflector movements and the velocity
perturbations.
domain tomography are smaller.
We explain these differences with the interference
between the reflector movements and the velocity
perturbations.
 |
The second example has a more complex background velocity.
A fast body (e.g. salt layer) is placed at depth,
below a shallow positive anomaly.
The shallow anomaly distorts
the time image of the fast body.
Because we assume that the shallow anomaly is not known,
the fast body is vertically distorted in
the ![]() domain starting model.
On the contrary, in the
domain starting model.
On the contrary, in the ![]() domain
the fast body has the same position in both
the starting and true model.
Figure
domain
the fast body has the same position in both
the starting and true model.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the true velocity model
and the reflector geometry in the
show the true velocity model
and the reflector geometry in the ![]() domain.
A contour plot of the starting model is
superimposed onto the true model
to illustrate the vertical distortion of the fast body.
A sample of zero-offset rays for both
the true (solid lines) and the starting models (dashed lines)
are superimposed onto the velocity model.
Figure
domain.
A contour plot of the starting model is
superimposed onto the true model
to illustrate the vertical distortion of the fast body.
A sample of zero-offset rays for both
the true (solid lines) and the starting models (dashed lines)
are superimposed onto the velocity model.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the equivalent
objects of Figure
shows the equivalent
objects of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , but in the
, but in the ![]() domain.
domain.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the linearization errors
for zero-offset reflections and 2 km offset reflections.
The solid lines show the error in the
show the linearization errors
for zero-offset reflections and 2 km offset reflections.
The solid lines show the error in the ![]() domain
and the dashed lines show the error in
domain
and the dashed lines show the error in ![]() domain.
The errors for
domain.
The errors for ![]() domain tomography are smaller,
although the differences are not that large.
domain tomography are smaller,
although the differences are not that large.
The final example is similar to the previous one,
except that the shallow anomaly is negative instead of positive.
In this case, surprisingly,
the linearization errors
shown in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are lower for the
are lower for the ![]() domain tomography.
than for the
domain tomography.
than for the ![]() domain tomography.
A possible explanation of these results is
that, by coincidence,
the additional errors
in the
domain tomography.
A possible explanation of these results is
that, by coincidence,
the additional errors
in the ![]() domain caused by the reflectors
and velocity model movements
have opposite sign
of the errors caused by the non-linear
behavior of the forward modeling.
domain caused by the reflectors
and velocity model movements
have opposite sign
of the errors caused by the non-linear
behavior of the forward modeling.
A comparison of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with Figure
with Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that the deep,
fast body
shifts vertically in
shows that the deep,
fast body
shifts vertically in ![]() domain
(Figure
domain
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
while it is stationary in the
)
while it is stationary in the ![]() (Figure
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Because of the depth shift of the fast body,
the velocity perturbations in the
).
Because of the depth shift of the fast body,
the velocity perturbations in the ![]() domain
are a dipole with a positive
and negative anomaly close to each other.
Usually tomographic inversions
strongly penalize features like a dipole
that are rapidly variant in space.
They are difficult to resolve
by tomography, and they can lead to divergence
if not kept in check.
Therefore correcting the
initial distortion
by a linearized inversion
would be difficult;
a full migration followed by reflector interpretation
are probably required.
domain
are a dipole with a positive
and negative anomaly close to each other.
Usually tomographic inversions
strongly penalize features like a dipole
that are rapidly variant in space.
They are difficult to resolve
by tomography, and they can lead to divergence
if not kept in check.
Therefore correcting the
initial distortion
by a linearized inversion
would be difficult;
a full migration followed by reflector interpretation
are probably required.