Synthetic data examples

In the following synthetic examples, I will compare migration implemented using analytical solutions of p_h with that using numerical solutions. Unless otherwise stated, all the examples are for anisotropic media ($\eta \gt$0), hinging on the fact that what works for anisotropic media should work for a subset of it, namely isotropic media.

 

imp2
Figure 8 Prestack time-migration impulse responses of an impulse at 1.8 s for a VTI medium with v=2.0 km/s and $\eta$=0.3. Left: the response was generated using the prestack phase-shift method with p_h estimated analytically (using the Shanks transform solution). Center: the response was generated also using the phase-shift method with p_h calculated numerically. Right: the response was generated by applying NMO, VTI DMO (Alkhalifah, 1996), and zero-offset phase-shift migration to the impulse.

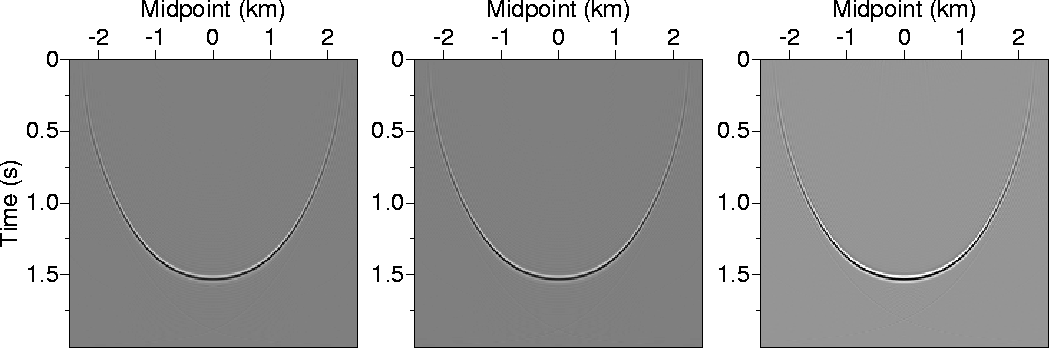Figure 8 shows impulse responses of an impulse input at 1.8 s into the prestack time migration algorithm, for a VTI medium with v=2.0 km/s and $\eta$=0.3. The offset considered here is 2.0 km. The first response was obtained using the prestack phase-shift migration with analytically derived values of p_h (using the 3-point Shanks-transform solution). The second response is also obtained using prestack phase-shift migration but now with numerically derived values of p_h. The final response resulted from inputing the impulse into an NMO correction algorithm, followed by the VTI dip-moveout (DMO) algorithm of Alkhalifah (1996), and then a VTI post-stack phase-shift migration. The DMO is based on the dip-decomposition method of Jakubowicz (1990). The responses are practically identical and therefore the output of applying these algorithms on real data should be similar. The advantage of the phase-shift method (the numerical version) is its ability to handle complex velocity functions.

 

impdiff
Figure 9 The difference between the prestack phase-shift migration responses shown in Figure 8 (the two on the left), plotted at the same amplitude scale as those in Figure 8.

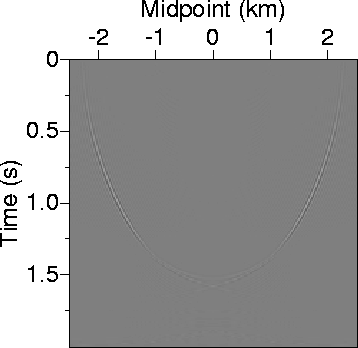Figure 9 shows the difference between the numerically derived p_h prestack migration response with the analytically derived one. The largest difference, as can be predicted from Figure 7, occurs at steep dips. Although kinematically the prestack and poststack approaches are similar, the DMO approach suffers from aliasing associated with improper sampling of the dip component, which appears when media with sharp velocity variations are treated. Such aliasing can somewhat be avoided by reducing the dip-decomposition sampling; however, this comes at larger cost of implementing the DMO. On the other hand, the response of the phase-shift migration does not show any of such aliasing artifacts, and the operator is thus cleaner.

 

model
Figure 10 Reflector model containing reflectors dipping at 0, 30, 45, 60, 75, and 90 degrees.

 

synti3
Figure 11 Common-offset synthetic data from the reflector model in Figure 10 for an offset of 2 km (left), and an offset of 4 km (right). The medium is VTI with velocity of 2.5 km/s and $\eta$=0.3.

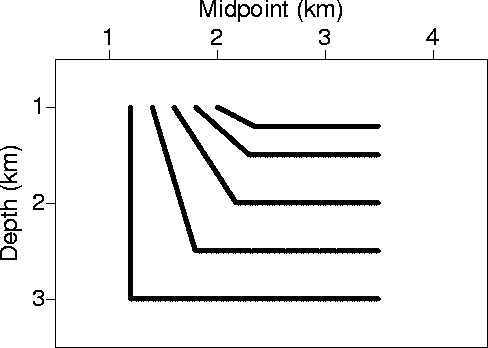
Figure 10 shows a model consisting of horizontal reflectors and dipping ones with dip angles ranging from 30 to 90 degrees at 15-degree intervals. The 90-degree reflector is not imaged in a homogeneous medium due to the limited aperture. Even the 75-degree one suffers from such a limit in the aperture. Figure 11 shows synthetic common-offset sections generated for a VTI medium with v=2.5 km/s and $\eta$=0.3. The left section corresponds to an offset of 2 km, the right one to an offset of 4 km. Figure 12 shows the result of prestack migration using the numerically derived p_h. For all practical purposes, the migrated images are identical and accurate.

 

migti3
Figure 12 Prestack phase-shift migrated section, using numerically derived p_h values, of the data in Figure 11 for an offset of 2 km (left), and an offset of 4 km (right). The mute level was somewhat relaxed to allow for maximum data exposure. Major portions of the right section would have not survived typical mute zones.

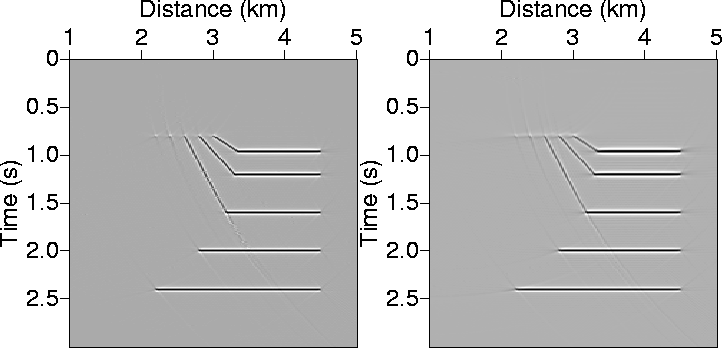Figure 13 shows the migration of Figure 11 using analytically derived values of p_h. Specifically, I am using the Shanks-transform 3-point solution of p_h because the medium is strongly anisotropic. The imaged section resembles the one obtained using numerical solutions of p_h.

 

miganti3
Figure 13 Prestack phase-shift migrated section using analytically derived p_h values of the data in Figure 11 for an offset of 2 km (left), and an offset of 4 km (right).

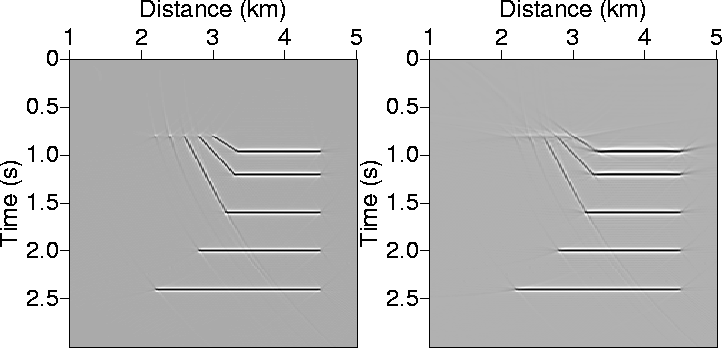The artifacts notable in the 4 km offset migrated section in Figure 13 are well within the typical mute zone, and they result from the limitations of the approximations to handle such large offset-to-depth ratios (>3) and such a strong anisotropy ($\eta$=0.3). For 4 km offset and v=2.5 km/s velocity, a typical mute time (a time where all samples prior to it are set to zero) is about 1.5 s.