




Next: CONNECTION OF THE LINEARIZED
Up: Fomel: Linearized Eikonal
Previous: REFERENCES
In this Appendix, I remind the reader how the eikonal equation is
derived from the wave equation. The derivation is classic and can be
found in many popular textbooks. See, for example, Cerveny et al. (1977).
Starting from the wave equation,
| 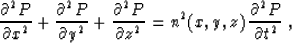 |
(8) |
we introduce a trial solution of the form
| 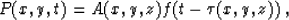 |
(9) |
where  is the eikonal, and A is the wave amplitude. The
waveform function f is assumed to be a high frequency
(discontinuous) signal. Substituting solution (9) into
equation (8), we arrive at the constraint
is the eikonal, and A is the wave amplitude. The
waveform function f is assumed to be a high frequency
(discontinuous) signal. Substituting solution (9) into
equation (8), we arrive at the constraint
| 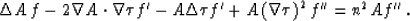 |
(10) |
Here 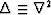 denotes the Laplacian operator.
Equation (10) is as exact as the initial wave equation
(8) and generally difficult to satisfy. However, we can
try to satisfy it asymptotically, considering each of the
high-frequency asymptotic components separately. The leading-order
component corresponds to the second derivative of the wavelet f''.
Isolating this component, we find that it is satisfied if and only if
the traveltime function
denotes the Laplacian operator.
Equation (10) is as exact as the initial wave equation
(8) and generally difficult to satisfy. However, we can
try to satisfy it asymptotically, considering each of the
high-frequency asymptotic components separately. The leading-order
component corresponds to the second derivative of the wavelet f''.
Isolating this component, we find that it is satisfied if and only if
the traveltime function 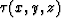 satisfies the eikonal equation
(1).
satisfies the eikonal equation
(1).
The next asymptotic order corresponds to the first derivative f'. It
leads to the amplitude transport equation
| 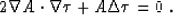 |
(11) |
The amplitude, defined by equation (11), is often referred
to as the amplitude of the zero-order term in the ray series. A series
expansion of the function f in high-frequency asymptotic components
produces recursive differential equations for the terms of higher
order. In practice, equation (11) is sufficiently accurate
for describing the major amplitude trends in most of the cases. It
fails, however, in some special cases, such as caustics and diffraction.
B





Next: CONNECTION OF THE LINEARIZED
Up: Fomel: Linearized Eikonal
Previous: REFERENCES
Stanford Exploration Project
11/11/1997