




Next: Examples
Up: Fomel: Regularization
Previous: Model-space regularization
In this section, I consider an alternative formulation of the
regularized least-square optimization.
We start again with the basic equation (1) and
introduce a residual vector r, defining it by the relationship
| 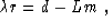 |
(10) |
where 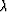 is a scaling parameter. Let us consider a compound model
is a scaling parameter. Let us consider a compound model
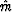 , composed of the model vector m itself and the residual
r. With respect to the compound model, equation (10) can be
rewritten as
, composed of the model vector m itself and the residual
r. With respect to the compound model, equation (10) can be
rewritten as
| ![\begin{displaymath}
\left[\begin{array}
{cc} L & \mbox{\unboldmath$\lambda$}I_d ...
...egin{array}
{c} m \\ r \end{array}\right] = G_d \hat{m} = d\;,\end{displaymath}](img16.gif) |
(11) |
where Gd is a row operator :
| ![\begin{displaymath}
G_d = \left[\begin{array}
{cc} L & \mbox{\unboldmath$\lambda$}I_d \end{array}\right]\;,\end{displaymath}](img17.gif) |
(12) |
and Id represents the data-space identity operator.
System (11) is clearly under-determined with respect to
the compound model 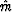 . If from all possible solutions of this
system we seek the one with the minimal power
. If from all possible solutions of this
system we seek the one with the minimal power 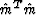 , the
formal (ideal) result takes the well-known form
, the
formal (ideal) result takes the well-known form
| ![\begin{displaymath}
<\!\!\hat{m}\!\!\gt = \left[\begin{array}
{c} <\!\!m\!\!\gt ...
...\unboldmath$\lambda$}^2 I_d\right)^{-1} d\end{array} \right]\;.\end{displaymath}](img19.gif) |
(13) |
To recall the derivation of formula (13), decompose the
effective model vector 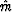 into two terms
into two terms
| 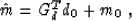 |
(14) |
where d0 and m0 are to be determined. First, we choose m0 to
be an orthogonal supplement to GdT d0. The orthogonality implies
that the objective function 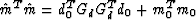 is minimized only when m0 = 0. To determine d0,
substitute (14) into equation (11) and solve
the corresponding linear system. The result takes the form of equation
(13).
is minimized only when m0 = 0. To determine d0,
substitute (14) into equation (11) and solve
the corresponding linear system. The result takes the form of equation
(13).
Let us show that estimate (13) is exactly equivalent to
estimate (9) from the ``trivial'' model-space
regularization. Consider the operator
| 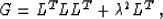 |
(15) |
which is a mapping from the data space to the model space. We can
group the multiplicative factors in formula (25) in two
different ways, as follows:
| 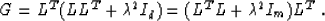 |
(16) |
Regrouping the terms in (16), we arrive at the exact
equality between the model estimates 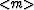 from equations
(13) and (9):
from equations
(13) and (9):
| 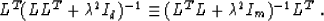 |
(17) |
To obtain equation (17), multiply both sides of
(16) by 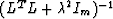 from the left and by
from the left and by
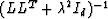 from the right. For
from the right. For 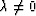 , both
these matrices are indeed invertible.
, both
these matrices are indeed invertible.
Not only the optimization estimate, but also the form of the objective
function, is exactly equivalent for both data-space and mode-space
cases. The objective function of model-space least squares 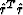 is connected with the data-space objective function
is connected with the data-space objective function 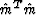 by the simple proportionality
by the simple proportionality
| 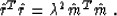 |
(18) |
This fact implies that the iterative methods of optimization - most
notably, the conjugate-gradient method Hestenes and Steifel (1952) - should
yield the same results for both formulations. Of course, this
conclusion doesn't take into account the numerical effects of
finite-precision computations.
To move to a more general (and interesting) case of ``non-trivial''
data-space regularization, we need to refer to the concept of model
preconditioning Nichols (1994). A preconditioning
operator P is used to introduce a new model x with the equality
| 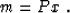 |
(19) |
Substituting definition (19) into formula
(11), we arrive at the following ``preconditioned'' form
of the operator Gd:
| ![\begin{displaymath}
\tilde{G}_d = \left[\begin{array}
{cc} LP & \mbox{\unboldmath$\lambda$}I_d \end{array}\right]\;.\end{displaymath}](img31.gif) |
(20) |
The operator 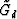 applies to the compound model vector
applies to the compound model vector
| ![\begin{displaymath}
\hat{x} = \left[\begin{array}
{c} x \\ r \end{array}\right]\;.\end{displaymath}](img33.gif) |
(21) |
Substituting formula (20) into (13) leads
to the following estimate for 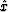 :
:
| ![\begin{displaymath}
<\!\!\hat{x}\!\!\gt = \left[\begin{array}
{c} <\!\!x\!\!\gt ...
...\unboldmath$\lambda$}^2 I_d\right)^{-1} d\end{array} \right]\;.\end{displaymath}](img35.gif) |
(22) |
Applying formula (19), we obtain the corresponding estimate
for the initial model m, as follows:
| 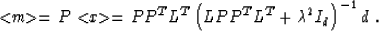 |
(23) |
Now we can show that estimate (23) is exactly equivalent to
formula (7) from the model-space regularization under the
condition
| 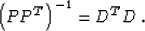 |
(24) |
Condition (24) assumes that the operator 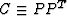 is invertible
is invertible![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) . Consider the operator
. Consider the operator
| 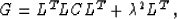 |
(25) |
which is another mapping from the data space to the model space.
Grouping the multiplicative factors in two different ways, we can
obtain the equality
| 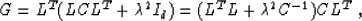 |
(26) |
or, in another form,
| 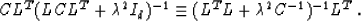 |
(27) |
The left-hand side of equality (27) is exactly the projection
operator from formula (23), and the right-hand side is the
operator from formula (7).
Comparing formulas (23) and (7), it is
interesting to note that we can turn a trivial regularization into a
non-trivial one by simply replacing the exact adjoint operator LT
by the operator C LT, which is a transformation from the data space
to the model space, followed by enforcing model correlations with the
operator C. This fact can be additionally confirmed by the equality
| 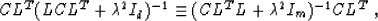 |
(28) |
which is derived analogously to formula (27). Iterative
optimization methods, which don't require exact adjoint operators
[e.g. the method of conjugate directions Fomel (1996)]
could be employed for the task.
Though the final results of the model-space and data-space
regularization are identical, the effect of preconditioning may alter
the behavior of iterative gradient-based methods, such as the method
of conjugate gradients. Though the objective functions are equal,
their gradients with respect to the model parameters are different.
Note, for example, that the first iteration of the model-space
regularization yields LT d as the model estimate regardless of the
regularization operator, while the first iteration of the model-space
regularization yields C LT d, which is a ``simplified'' version of
the model. Since iteration to the exact solution is never achieved in
the large-scale problems, the results of iterative optimization may
turn out quite differently. Harlan (1995) points out that the two
components of the model-space regularization [equations
(1) and (2)] conflict with each other: the
first one enforces ``details'' in the model, while the second one
tries to smooth them out. He describes the advantage of
preconditioning:
The two objective functions produce different results when
optimization is incomplete. A descent optimization of the original
(model-space - S.F. ) objective function will begin with
complex perturbations of the model and slowly converge toward an
increasingly simple model at the global minimum. A descent
optimization of the revised (data-space - S.F. ) objective
function will begin with simple perturbations of the model and
slowly converge toward an increasingly complex model at the global
minimum. ...A more economical implementation can use fewer
iterations. Insufficient iterations result in an insufficiently
complex model, not in an insufficiently simplified model.
Examples in the next section illustrate these conclusions.





Next: Examples
Up: Fomel: Regularization
Previous: Model-space regularization
Stanford Exploration Project
11/11/1997
![]() . If from all possible solutions of this
system we seek the one with the minimal power
. If from all possible solutions of this
system we seek the one with the minimal power ![]() , the
formal (ideal) result takes the well-known form
, the
formal (ideal) result takes the well-known form
![\begin{displaymath}
<\!\!\hat{m}\!\!\gt = \left[\begin{array}
{c} <\!\!m\!\!\gt ...
...\unboldmath$\lambda$}^2 I_d\right)^{-1} d\end{array} \right]\;.\end{displaymath}](img19.gif)
![]() is connected with the data-space objective function
is connected with the data-space objective function ![]() by the simple proportionality
by the simple proportionality
![\begin{displaymath}
<\!\!\hat{x}\!\!\gt = \left[\begin{array}
{c} <\!\!x\!\!\gt ...
...\unboldmath$\lambda$}^2 I_d\right)^{-1} d\end{array} \right]\;.\end{displaymath}](img35.gif)
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) . Consider the operator
. Consider the operator