




Next: Data-space regularization
Up: Fomel: Regularization
Previous: Introduction
Let us denote the linear forward modeling operator by L. Then
the basic matrix equation to be inverted is
| 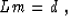 |
(1) |
where m stands for the model vector, and d
represents the data vector.
Quite often the size of the data space is smaller than the desired
size of the model space. This is typical for some interpolation
problems Claerbout (1992, 1994), but may also
be the case in tomographic problems. Even if the data size is larger
than the model size, certain components of the model m may not be
fully constrained by equation (1). In interpolation
applications, this situation corresponds to empty bins in the model
space. In tomography applications, it corresponds to shadow zones in
the model, not illuminated by the tomographic rays.
Model-space regularization suggests adding equations to system
(1) to obtain a fully constrained (well-posed) inverse
problem. These additional equations are based on prior assumptions
about the model and typically take the form
| 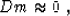 |
(2) |
where D represents the imposed condition in the form of a linear
operator. In many applications, D can be thought of as a filter,
enhancing ``bad'' components in the model, or as a differential
equation that we assume the model should satisfy.
The full system of equations (1)-(2) can be
written in a short notation as
| ![\begin{displaymath}
G_m m = \left[\begin{array}
{c} L \\ \mbox{\unboldmath$\lam...
...\left[\begin{array}
{c} d \\ 0 \end{array}\right] = \hat{d}\;,\end{displaymath}](img3.gif) |
(3) |
where 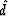 is the effective data vector:
is the effective data vector:
| ![\begin{displaymath}
\hat{d} = \left[\begin{array}
{c} d \\ 0 \end{array}\right]\;,\end{displaymath}](img5.gif) |
(4) |
Gm is a column operator:
| ![\begin{displaymath}
G_m = \left[\begin{array}
{c} L \\ \mbox{\unboldmath$\lambda$}D \end{array}\right]\;,\end{displaymath}](img6.gif) |
(5) |
and 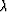 is a scaling parameter. The subscript m stands for
model space to help us distinguish Gm from the analogous
data-space operator, introduced in the next section.
is a scaling parameter. The subscript m stands for
model space to help us distinguish Gm from the analogous
data-space operator, introduced in the next section.
Now that the inverse problem (3) is fully
constrained, we can solve it by means of unconstrained least-square
optimization, minimizing the squared power 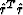 of
the compound residual vector
of
the compound residual vector
| ![\begin{displaymath}
\hat{r} = \hat{d} - G_m m =
\left[\begin{array}
{c} d - L m\\ - \mbox{\unboldmath$\lambda$}D m \end{array}\right]\;.\end{displaymath}](img9.gif) |
(6) |
The formal solution of the regularized optimization problem has the
known form
| 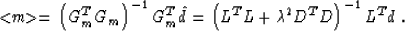 |
(7) |
To recall the derivation of formula (7), consider the
objective function
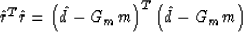
and take its partial derivative with respect
to the model vector m. Setting the derivative equal to zero leads to
the normal equations
| 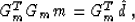 |
(8) |
whose solution has the form of formula (7).
For the sake of simplicity, we will consider separately a ``trivial''
regularization, which seeks the smallest possible model from all the
models, defined by equation (1). For this form of
regularization, DT D is an identity operator. If we denote the
model-space identity operator by Im, the least-square estimate in
this case takes the form
| 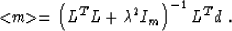 |
(9) |





Next: Data-space regularization
Up: Fomel: Regularization
Previous: Introduction
Stanford Exploration Project
11/11/1997
![]() of
the compound residual vector
of
the compound residual vector
![]()