




Next: About this document ...
Up: Claerbout: Preconditioning and scalingPreconditioning
Previous: HOW MUCH DAMPING?
A problem arises with partitioned operators.
Here we are fitting observed data to theoretical data
where there are two classes of model parameters
 and
and  .We seek to minimize
the norm of the residual
.We seek to minimize
the norm of the residual  defined by
defined by
| ![\begin{displaymath}
\bold 0 \quad\approx\quad \bold r \quad=\quad
\left[
\alpha ...
..._1/\alpha \\ \bold m_2/\beta
\end{array}\right] \ - \ \bold d\end{displaymath}](img33.gif) |
(9) |
where  and
and 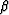 are arbitrary scaling constants.
The residual is independent of
are arbitrary scaling constants.
The residual is independent of  and
and 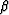 ,but when we ``solve" this system using (as we must)
the idea that
,but when we ``solve" this system using (as we must)
the idea that  ,we see the result depends on
,we see the result depends on  and
and 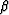 ,namely it contains
,namely it contains  and
and 
| ![\begin{displaymath}
\left[
\begin{array}
{l}
\hat \bold m_1/\alpha \\ \hat \b...
...alpha \bold F' \\ \beta \bold B'
\end{array}\right]
\ \bold d\end{displaymath}](img39.gif) |
(10) |
Let us find the best  and
and 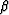 .Inserting the image (10)
into the residual (9)
we get
.Inserting the image (10)
into the residual (9)
we get
|  |
(11) |
| (12) |
| (13) |
which defines two vectors  and
and 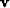 .
.
We find the best scaling factors by
setting to zero the derivative of  with respect to
with respect to  and
and 
| ![\begin{displaymath}
\bold 0
\quad=\quad
\left[
\begin{array}
{rr}
\bold u'\bold...
...y}
{c}
\bold u'\bold d \\ \bold v'\bold d \end{array} \right]\end{displaymath}](img44.gif) |
(14) |
solving gives
| ![\begin{displaymath}
\left[
\begin{array}
{c}
\alpha^2 \\ \beta^2 \end{array} \...
...y}
{c}
\bold u'\bold d \\ \bold v'\bold d \end{array} \right]\end{displaymath}](img45.gif) |
(15) |
I believe it can be shown that the values
 and
and  are positive.
are positive.
Recalling that
 and
and
 ,let us now define
,let us now define
 and
and
 so
so
 and
and
 .
.
In imaging applications we customarily ignore the scaling factor
which is the common part of  and
and 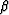 ,namely, the denominator determinant in (15).
We have the proportions
,namely, the denominator determinant in (15).
We have the proportions
|  |
(16) |
| (17) |
| (18) |
A deeper problem of interest
arises when we seek the best diagonal matrix scaling.
Then we replace  with two diagonal matrices, one before and one after
with two diagonal matrices, one before and one after 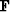 .Likewise with
.Likewise with 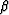 and
and 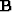 .We need help finding those four diagonal matrices.
.We need help finding those four diagonal matrices.





Next: About this document ...
Up: Claerbout: Preconditioning and scalingPreconditioning
Previous: HOW MUCH DAMPING?
Stanford Exploration Project
11/11/1997

![]() with respect to
with respect to ![]() and
and ![]()
![]() and
and
![]() ,let us now define
,let us now define
![]() and
and
![]() so
so
![]() and
and
![]() .
.![]() and
and ![]() ,namely, the denominator determinant in (15).
We have the proportions
,namely, the denominator determinant in (15).
We have the proportions

![]() with two diagonal matrices, one before and one after
with two diagonal matrices, one before and one after ![]() .Likewise with
.Likewise with ![]() and
and ![]() .We need help finding those four diagonal matrices.
.We need help finding those four diagonal matrices.