




Next: ROW PARTITIONED OPERATORS
Up: Claerbout: Preconditioning and scalingPreconditioning
Previous: ROUGHENERS AND SMOOTHERS
We often need to damp the solutions to least squares problems.
We have a fitting problem (regression) with the two goals:
| 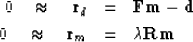 |
(5) |
| (6) |
where 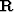 is a roughening operator.
How big should
is a roughening operator.
How big should 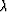 be?
Suppose in human terms we'd like ``half''
the properties of the solution to come from the fitting
and ``half'' to come from the damping.
How might we define what we mean by ``half''?
We can start by considering balancing the two residual vectors
be?
Suppose in human terms we'd like ``half''
the properties of the solution to come from the fitting
and ``half'' to come from the damping.
How might we define what we mean by ``half''?
We can start by considering balancing the two residual vectors
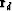 and
and 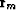 .
.
| 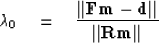 |
(7) |
Another approach is to balance the gradients.
The gradient is the ``force'' on the solution m.
| 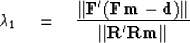 |
(8) |
where 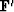 is the transpose of
is the transpose of 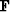 and likewise for
and likewise for 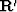 .I suspect that
.I suspect that 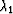 is the better choice for
is the better choice for 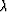 but a little more experience would add confidence.
but a little more experience would add confidence.





Next: ROW PARTITIONED OPERATORS
Up: Claerbout: Preconditioning and scalingPreconditioning
Previous: ROUGHENERS AND SMOOTHERS
Stanford Exploration Project
11/11/1997