




Next: Estimating the spatial prediction
Up: ESTIMATION OF SPATIAL PREDICTION
Previous: Wavefield composed of one
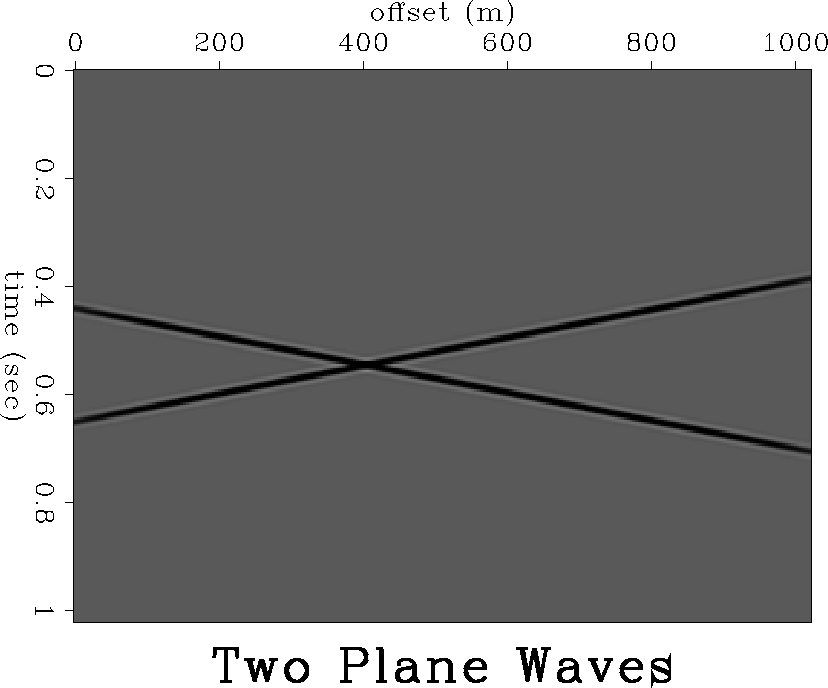
If we have two plane waves, the wavefield (Figure 6) can be
expressed by
| 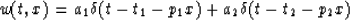 |
(11) |
two-plane-wave
Figure 6 A synthetic wavefield composed of two plane waves.
|
|  |





In the f-x domain, it has another expression
| 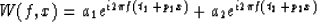 |
(12) |
Or
where 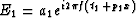 and
and 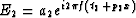 .The adjacent trace can be expressed by
.The adjacent trace can be expressed by
| 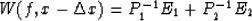 |
(14) |
Now we cannot predict one trace from another trace, since there are two
unknown propagators. Consequently, we need the information from another trace.
| 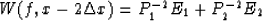 |
(15) |
Equation (14) and (15) can be solved for the propagators. But in
reality, we do not know p1 and p2. So we cannot get the explicit
form of the propagators. We must use another form of parameter to link the
the different traces together, which is called a spatial prediction filter.
If we have trace 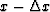 and trace
and trace 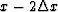 , our aim is
to predict trace x. Assume there is a relation between the three traces:
, our aim is
to predict trace x. Assume there is a relation between the three traces:
| 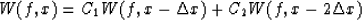 |
(16) |
Substituting Ws with equations (13), (14) and (15), we get
|
E1+E2 = C1(P-11E1+P-12E2)+C2(P-21E1+P-22E2)
|
(17) |
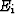 can be any value, as long as it is a plane wave. Therefore,
equation (17) holds for all of E1 and E2. In particular, we have
can be any value, as long as it is a plane wave. Therefore,
equation (17) holds for all of E1 and E2. In particular, we have
| 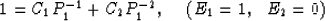 |
(18) |
| 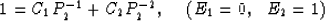 |
(19) |
Solving this linear equation, we find the relation between 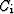 and
and
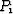 (i=1,2). That is
(i=1,2). That is
|  |
(20) |
Like the one plane wave case, all above deductions have nothing to do with the
gridding scheme. All the results are effective for both cases. The differences
between the two gridding schemes are
We can extend our deduction to N plane waves (see the Appendix) and we can get
similar results: for FIG, coefficient 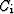 is frequency-dependent;
for FDG,
is frequency-dependent;
for FDG, 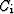 is frequency-independent. This is the basis of
estimating the spatial prediction filter.
is frequency-independent. This is the basis of
estimating the spatial prediction filter.





Next: Estimating the spatial prediction
Up: ESTIMATION OF SPATIAL PREDICTION
Previous: Wavefield composed of one
Stanford Exploration Project
11/11/1997

![]() and trace
and trace ![]() , our aim is
to predict trace x. Assume there is a relation between the three traces:
, our aim is
to predict trace x. Assume there is a relation between the three traces:
![]() is frequency-dependent;
for FDG,
is frequency-dependent;
for FDG, ![]() is frequency-independent. This is the basis of
estimating the spatial prediction filter.
is frequency-independent. This is the basis of
estimating the spatial prediction filter.