Next: CONCLUSIONS
Up: CROSSWELL TOMOGRAPHY APPLICATION
Previous: CROSSWELL TOMOGRAPHY APPLICATION
For the LSQR algorithm, it is easy to check the trace of the effective
operator since it is just the sum of the squares of the elements
in the resulting bidiagonal matrix. To test the ideas of the preceding
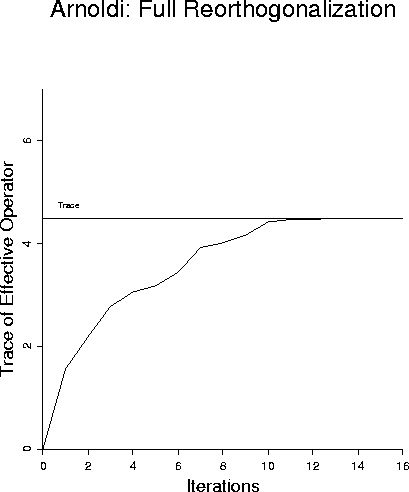
section, we first perform an LSQR inversion while imposing full
reorthogonalization Arnoldi (1951) at each step. Doing so, we obtain
Figure 5, showing that the effective operator trace converges
monotonically to the true trace from below as expected.
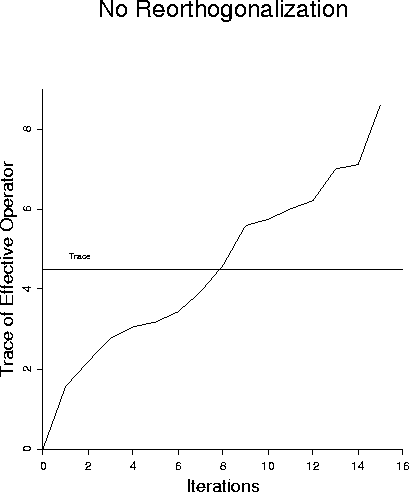
In contrast, Figure 6 shows that without reorthogonalization
the trace of the effective operator has already exceeded the
upper bound -- thus demonstrating that the eighth direction
vector found by LSQR has at least some component parallel to one
of the earlier vectors and also along some eigenvector with large eigenvalue.
Observing the later behavior of this curve, regions of small slopes
may correspond to allowable (orthogonal) direction vectors, but the regions of
large slope must be resampling the regions of the vector space with
the largest eigenvalues. This observation shows that the rebirth of
nonorthogonal vectors does not happen just at the eighth iteration, but
is a recurring problem.
These two examples show clearly that full reorthogonalization works very well
and that failure to do any reorthogonalization can lead to serious problems with
the set of direction vectors generated by such schemes.
To make progress, we want to know whether full reorthogonalization
is required, or whether some type of partial reothogonalization
(which will presumably be cheaper) might be equally or almost as
effective as full reorthogonalization. We want to explore the
tradeoffs between cost of the partial reorthogonalization and
the benefits to be derived from it. Figures 7-11 explore these issues.
sumarnoldi
Figure 5
LSQR with full (Arnoldi) reorthogonalization.
 sum000
sum000
Figure 6
LSQR with no reorthogonalization.

Figures 7-9 refer to the same model considered in Figures 1-6.
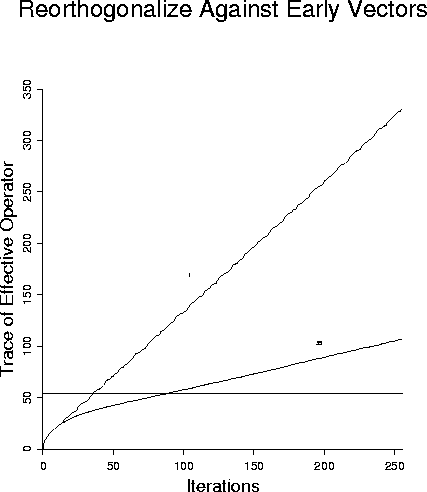
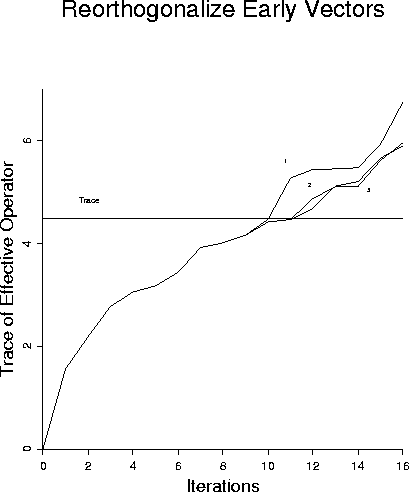
Figure 7 shows that orthogonalizing against the first 1, 2, or 3 vectors
improves the results progressively, the more vectors are used for
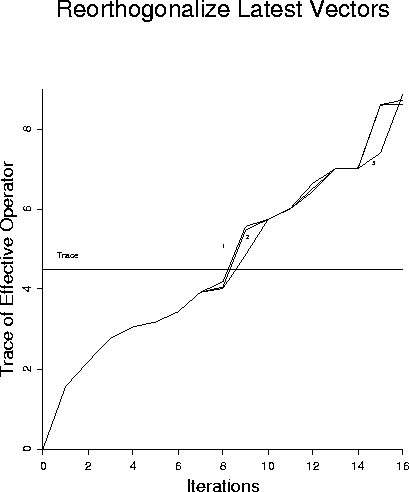
the reorthogonalization. Figure 8 shows that reorthogonalization
against the 1, 2, or 3 most recently generated vectors does not work
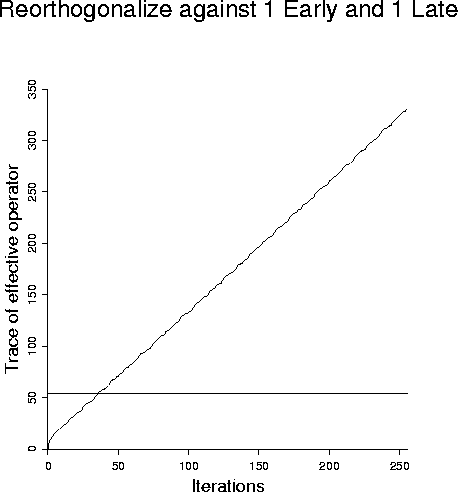
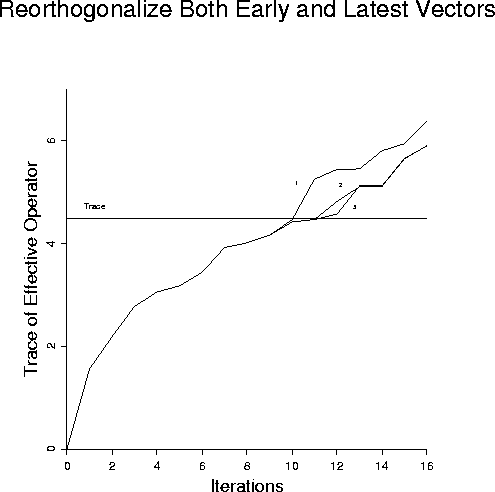
as well as the previous Figure. Reorthogonalizing against both 1, 2, or 3 early
and late vectors gives virtually identical results in Figure 9 as those results
observed in Figure 7.
sum310
Figure 7
LSQR with partial reorthogonalization - first one, two, or three.
 sum301
sum301
Figure 8
LSQR with partial reorthogonalization - last one, two, or three.
 sum311
sum311
Figure 9
LSQR with partial reorthogonalization - using both first and last
one, two, or three.

Figures 10 and 11 refer to a model of 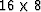 cells similar to
that considered earlier by Berryman 1990.
Figure 10 shows that reorthogonalizing against only the first and last
vectors generated in the iteration sequence is quite ineffective
at reducing the nonorthogonal vectors generated.
Figure 11 shows that reorthogonalizing against the first 35 vectors
produces a major improvement, without significant orthogonalization
problems out to 90 iterations, instead of less than 35 iterations before
problems arise with only one vector reothogonalization.
cells similar to
that considered earlier by Berryman 1990.
Figure 10 shows that reorthogonalizing against only the first and last
vectors generated in the iteration sequence is quite ineffective
at reducing the nonorthogonal vectors generated.
Figure 11 shows that reorthogonalizing against the first 35 vectors
produces a major improvement, without significant orthogonalization
problems out to 90 iterations, instead of less than 35 iterations before
problems arise with only one vector reothogonalization.
ex111
Figure 10
LSQR with partial reorthogonalization - using first and last vector.
 ex3510
ex3510
Figure 11
LSQR with partial reorthogonalization - using first or first 35 vectors.

We conclude that reorthogonalization is effective and the partial
reorthogonalization is most effective when the vectors chosen for
the reorthogonalization set are those from the early part of the
iteration sequence. The reason that these vectors are best to
use is presumably because they correspond to directions that
have components parallel to directions in the space that are
eigenvectors of the operator being inverted with largest eigenvalues.
These vectors like to be reborn in this process and reorthogonalization
is an effective means of preventing multiply copies of the same
dominant vectors from recurring in the iteration sequence.





Next: CONCLUSIONS
Up: CROSSWELL TOMOGRAPHY APPLICATION
Previous: CROSSWELL TOMOGRAPHY APPLICATION
Stanford Exploration Project
11/11/1997

![]() cells similar to
that considered earlier by Berryman 1990.
Figure 10 shows that reorthogonalizing against only the first and last
vectors generated in the iteration sequence is quite ineffective
at reducing the nonorthogonal vectors generated.
Figure 11 shows that reorthogonalizing against the first 35 vectors
produces a major improvement, without significant orthogonalization
problems out to 90 iterations, instead of less than 35 iterations before
problems arise with only one vector reothogonalization.
cells similar to
that considered earlier by Berryman 1990.
Figure 10 shows that reorthogonalizing against only the first and last
vectors generated in the iteration sequence is quite ineffective
at reducing the nonorthogonal vectors generated.
Figure 11 shows that reorthogonalizing against the first 35 vectors
produces a major improvement, without significant orthogonalization
problems out to 90 iterations, instead of less than 35 iterations before
problems arise with only one vector reothogonalization.