Next: Tests of orthogonalization
Up: Berryman & Fomel: Iterative
Previous: IMPORTANCE OF MAINTAINING ORTHOGONALITY
Figures 1-4 provide some numerical examples comparing and contrasting the
results obtained using standard SVD resolution calculations with
the LSQR Paige and Saunders (1982) resolution calculations described in an earlier paper
Berryman (1994). We
consider a  model using strictly crosswell data, so there
are 16 source/receiver pairs as well as 16 cells in 2D. Model
slowness values are shown in the upper block of each figure, while
diagonal resolution values are shown in the lower block. The first two
examples (Figures 1 and 2) show results for the actual model used to compute the
traveltime data [see Berryman 1990 for a description of the code used
to generate both the forward and inverse solutions]. The second two examples
(Figures 3 and 4) show results obtained after 15 iterations of the reconstruction code of
Berryman 1990. The LSQR resolution examples (Figures 2 and 4) were computed
using ten iterations of the LSQR algorithm, so the maximum size of the
resolved model vector space has dimension ten. To aid in the comparison, the
SVD resolution examples use only the 10 eigenvectors associated with
the 10 largest eigenvalues of the ray-path matrix. We find the results
are in qualitatively good agreement. Better quantitative agreement is
not anticipated because the 10-dimensional vector spaces spanned by these two
approximations, although having large regions of overlap, will nevertheless
almost always differ to some degree.
model using strictly crosswell data, so there
are 16 source/receiver pairs as well as 16 cells in 2D. Model
slowness values are shown in the upper block of each figure, while
diagonal resolution values are shown in the lower block. The first two
examples (Figures 1 and 2) show results for the actual model used to compute the
traveltime data [see Berryman 1990 for a description of the code used
to generate both the forward and inverse solutions]. The second two examples
(Figures 3 and 4) show results obtained after 15 iterations of the reconstruction code of
Berryman 1990. The LSQR resolution examples (Figures 2 and 4) were computed
using ten iterations of the LSQR algorithm, so the maximum size of the
resolved model vector space has dimension ten. To aid in the comparison, the
SVD resolution examples use only the 10 eigenvectors associated with
the 10 largest eigenvalues of the ray-path matrix. We find the results
are in qualitatively good agreement. Better quantitative agreement is
not anticipated because the 10-dimensional vector spaces spanned by these two
approximations, although having large regions of overlap, will nevertheless
almost always differ to some degree.
casea
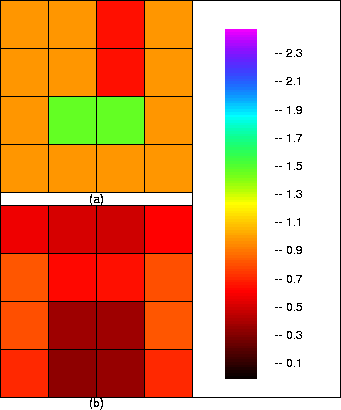
Figure 1
Target model slowness (a) and resolution (b) for truncated SVD using 10 largest eigenvalues.
 caseb
caseb
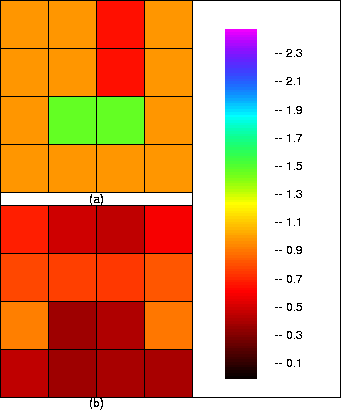
Figure 2
Target model slowness (a) and resolution (b) for LSQR after 10 iteratons.
 casec
casec
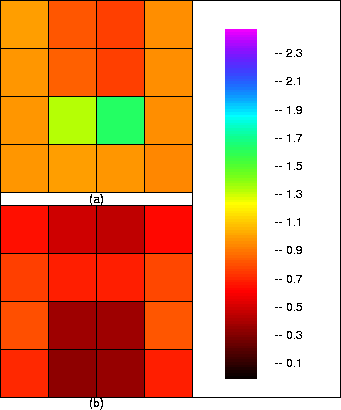
Figure 3
Slowness (a) and resolution (b) for truncated SVD using 10 largest eigenvalues.
 cased
cased
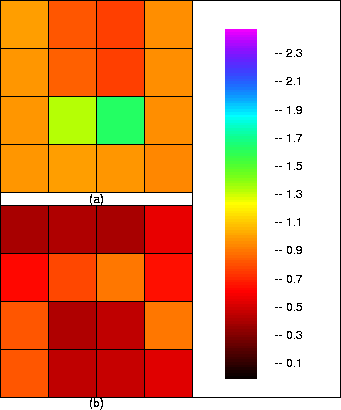
Figure 4
Reconstructed slowness (a) and resolution (b) for LSQR after 10 iterations.






Next: Tests of orthogonalization
Up: Berryman & Fomel: Iterative
Previous: IMPORTANCE OF MAINTAINING ORTHOGONALITY
Stanford Exploration Project
11/11/1997
![]() model using strictly crosswell data, so there
are 16 source/receiver pairs as well as 16 cells in 2D. Model
slowness values are shown in the upper block of each figure, while
diagonal resolution values are shown in the lower block. The first two
examples (Figures 1 and 2) show results for the actual model used to compute the
traveltime data [see Berryman 1990 for a description of the code used
to generate both the forward and inverse solutions]. The second two examples
(Figures 3 and 4) show results obtained after 15 iterations of the reconstruction code of
Berryman 1990. The LSQR resolution examples (Figures 2 and 4) were computed
using ten iterations of the LSQR algorithm, so the maximum size of the
resolved model vector space has dimension ten. To aid in the comparison, the
SVD resolution examples use only the 10 eigenvectors associated with
the 10 largest eigenvalues of the ray-path matrix. We find the results
are in qualitatively good agreement. Better quantitative agreement is
not anticipated because the 10-dimensional vector spaces spanned by these two
approximations, although having large regions of overlap, will nevertheless
almost always differ to some degree.
model using strictly crosswell data, so there
are 16 source/receiver pairs as well as 16 cells in 2D. Model
slowness values are shown in the upper block of each figure, while
diagonal resolution values are shown in the lower block. The first two
examples (Figures 1 and 2) show results for the actual model used to compute the
traveltime data [see Berryman 1990 for a description of the code used
to generate both the forward and inverse solutions]. The second two examples
(Figures 3 and 4) show results obtained after 15 iterations of the reconstruction code of
Berryman 1990. The LSQR resolution examples (Figures 2 and 4) were computed
using ten iterations of the LSQR algorithm, so the maximum size of the
resolved model vector space has dimension ten. To aid in the comparison, the
SVD resolution examples use only the 10 eigenvectors associated with
the 10 largest eigenvalues of the ray-path matrix. We find the results
are in qualitatively good agreement. Better quantitative agreement is
not anticipated because the 10-dimensional vector spaces spanned by these two
approximations, although having large regions of overlap, will nevertheless
almost always differ to some degree.