| |
(95) |
| |
(96) |
|
vlcfds
Figure 12 Finite-difference scheme for the velocity continuation equation. A stable propagation is either forward in velocity and backward in time (left plot) or backward in velocity and forward in time (right plot). | 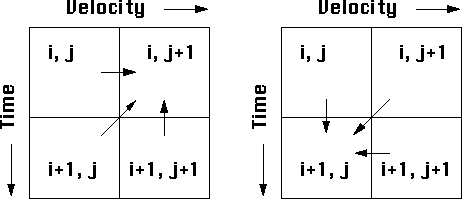 |
The following simple ratfor program implements the finite-difference velocity continuation. It is slightly modified from Jon Claerbout's original version and has a more straightforward loop structure than Zhiming Li's Caso15 program.
subroutine velconx(adj,add,inv, v1,v2,t0, nt,nx,nv, dt,dx, p1,p2) integer adj,add,inv, nt,nx,nv, it,ix,iv, it1,it2,its, iv1,iv2,ivs real v1,v2,t0, dt,dx,dv, v,t, a,a0,b, b1,b2,offd,diag real p1(nt,nx),p2(nt,nx) temporary real l(nx),r(nx),ld(nx),rd(nx),rhs(nx),pt(nx,nt)if (v1 <= v2) call erexit('unstable velocity continuation') call adjnull(adj, add,p1,nt*nx,p2,nt*nx) dv = (v1-v2)/nv; a0=(4.*dx*dx)/(dt*dv); b=0.14867678
if (adj==0) {do ix=1,nx { do it=1,nt{ pt(ix,it)=p1(it,ix)}} iv1=nv; iv2= 1; ivs=-1; it1= 2; it2=nt; its= 1} else {do ix=1,nx { do it=1,nt{ pt(ix,it)=p2(it,ix)}} iv1=1; iv2=nv; ivs= 1; it1=nt; it2= 2; its=-1}
do iv=iv1,iv2,ivs {v=sqrt(v2+(iv-0.5)*dv); call null(rhs,nx) do it=it1,it2,its {t=t0+dt*(it-1) if (inv==0) {t=sqrt(t)*v; a=a0/t} # Pseudounitary else if (inv==1) {t=t*v; a=a0/v} # Claerbout's else if (inv==2) {a=a0/(t*v); t=v} # True-amplitude b1=b*a+t; b2=b*a-t; offd=a-b2; diag=a-2*b2 call copy(nx,pt(1,it),l); call diffxx(nx,l,ld) do ix=1,nx {rhs(ix) = rhs(ix) + a*l(ix) + b1*ld(ix)} call rtris(nx,offd,b2,diag,b2,offd,rhs,r); call diffxx(nx,r,rd) do ix=1,nx {rhs(ix) = a*r(ix) + b1*rd(ix) - a*l(ix) - b2*ld(ix)} call copy(nx,r,pt(1,it)) }}
if (adj==0) {do ix=1,nx { do it=1,nt{ p2(it,ix)=p2(it,ix)+pt(ix,it)}}} else {do ix=1,nx { do it=1,nt{ p1(it,ix)=p1(it,ix)+pt(ix,it)}}} return; end
subroutine diffxx(nx,f,fxx) integer ix,nx real f(nx),fxx(nx) do ix=2,nx-1 fxx(ix) = f(ix-1) -2*f(ix) +f(ix+1) ix=1; fxx(ix) = f(1) -2*f(ix) +f(ix+1) ix=nx; fxx(ix) = f(ix-1) -2*f(ix) +f(nx) return; end
The parameter adj controls the direction of propagation. It is
equal to zero for backward propagation, which corresponds to the
modeling (demigration) operator. The parameter inv controls the
amplitude behavior by introducing time-dependent divisors to equation
(95). For inv=1, the program implements
Claerbout's velocity continuation equation. For inv=2, it
implements the modified equation (55). The value of
inv=0 corresponds to the intermediate case. It leads to the
pseudounitary velocity continuation, for which the reverse
continuation is the exact adjoint operator
Fomel (1996). We can easily test different types of
amplitude behavior with the dot-product test and its modifications.
The parameter b is required for the ``1/6 trick'' introduced by
Claerbout 1985 to increase the accuracy
of the second-derivative operator ![]() in (95). The
second-order difference in subroutine diffxx implies simple
zero-slope boundary conditions on the midpoint coordinate. The call to
rtris solves the triadiagonal system.
in (95). The
second-order difference in subroutine diffxx implies simple
zero-slope boundary conditions on the midpoint coordinate. The call to
rtris solves the triadiagonal system.
In order to test the performance of the finite-difference velocity continuation method, I use a simple synthetic model from Basic Earth Imaging Claerbout (1995). The ``reflectivity'' model is shown in Figure 13. It contains several features challenging the migration performance: dipping beds, unconformity, syncline, anticline, and fault.
|
vlcmod
Figure 13 Synthetic model for testing finite-difference migration by velocity continuation. |  |
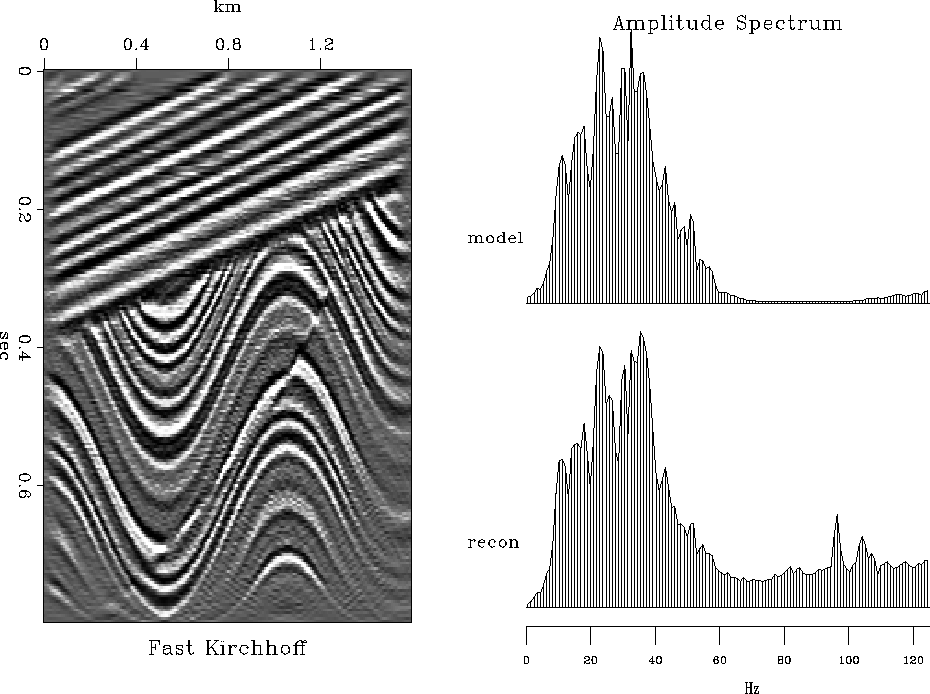
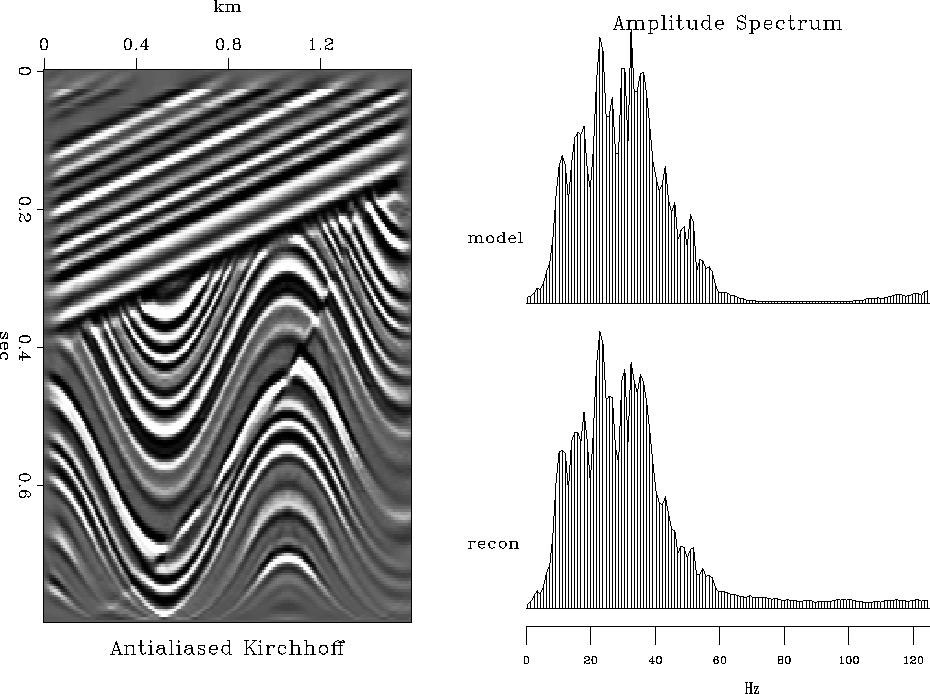
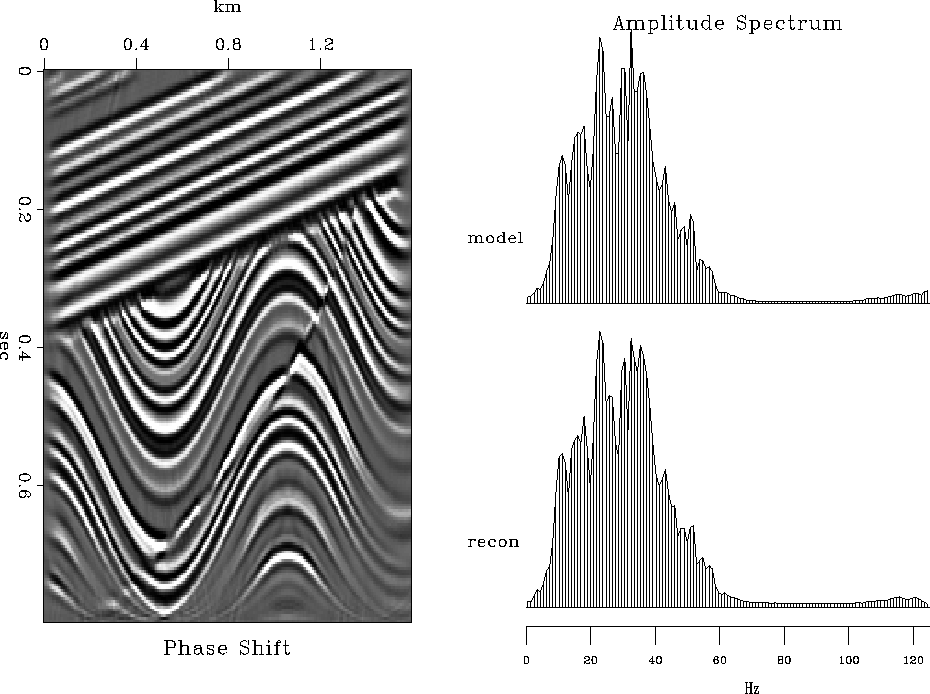
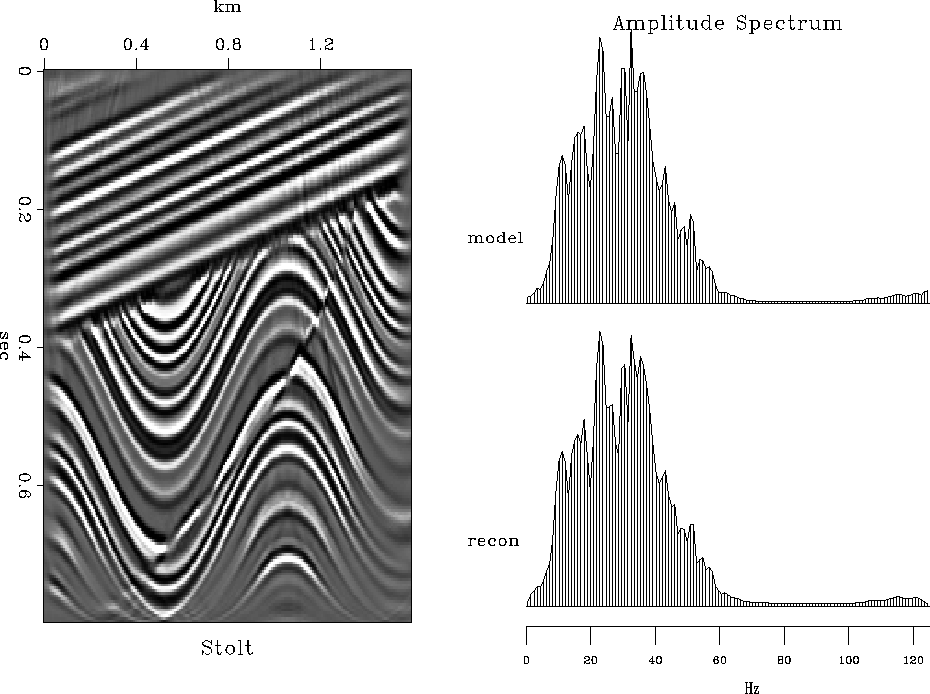
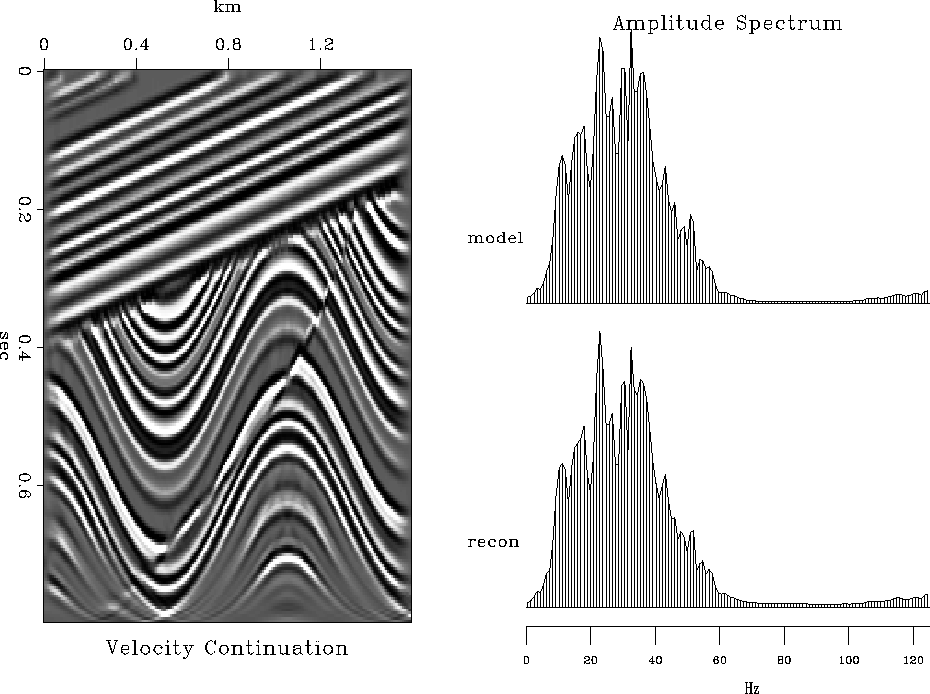
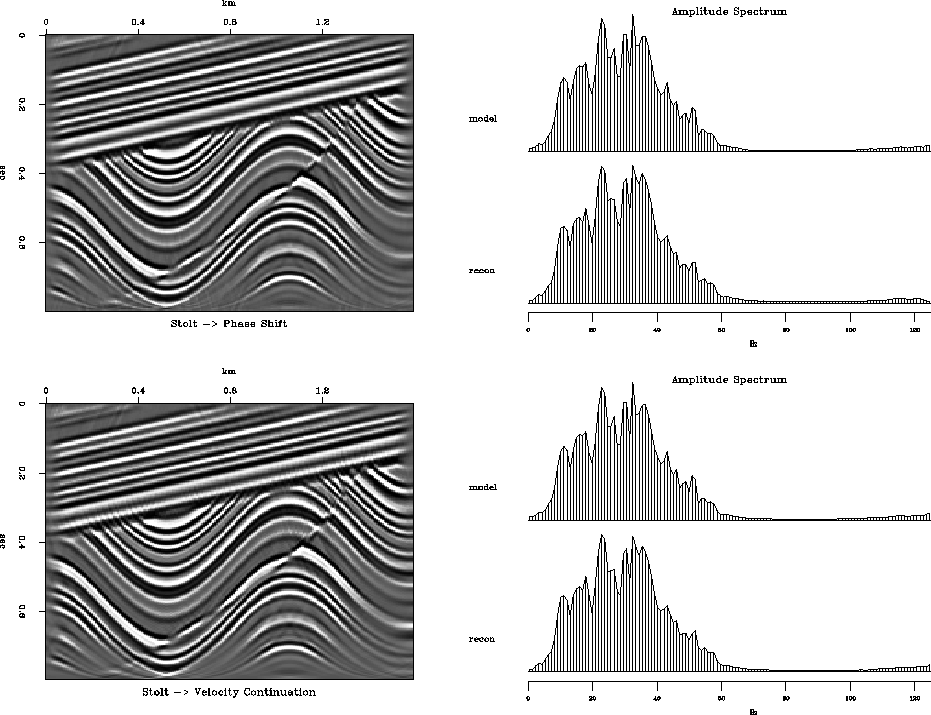
The following series of figures compares invertability of different migration methods. In all cases, constant-velocity modeling (demigration) by the adjoint operator was followed by migration with the correct velocity v=1500 m/sec. Figures 14, 15, 16, 17 show the results of modeling and migration with fast (nearest-neighbor) Kirchhoff, antialiased Kirchhoff Fomel and Biondi (1995), phase-shift (Gazdag), and Stolt methods respectively. These figures should be compared with Figure 18, showing the analogous result of the finite-difference velocity continuation. The comparison reveals a remarkable invertability of velocity continuation, which reconstructs accurately the main features and frequency content of the model. Since the forward operators were different for different migrations, this comparison did not test the migration properties themselves. For such a test, I compare the results of the phase-shift and velocity-continuation migrations after Stolt modeling. The result of velocity continuation, shown in Figure 19 is at least as accurate as that of the phase-shift method.
 |
 |
 |
 |
 |
 |
We can conclude that finite-difference velocity continuation is an attractive migration method. It possesses remarkable invertability properties, which might be useful in some applications. According to Li 1986, the computational speed of this method compares favorably with that of Stolt migration. The advantage is apparent for cascaded migration or migration with multiple velocity models. In these cases, the cost of Stolt migration increases in direct proportion with the number of velocity models, while the cost of velocity continuation stays the same.