REFERENCES

Beasley, C., Lynn, W., Larner, K., and Nguyen, H., 1988, Cascaded frequency-wavenumber migration - removing the restrictions on depth-varying velocity: Geophysics, 53, no. 7, 881-893.

Belonosova, A. V., and Alekseev, A. S., 1967, About one formulation of the inverse kinematic problem of seismics for a two-dimensional continuously heterogeneous medium:, in Some methods and algorithms for interpretation of geophysical data (in Russian) Nauka, 137-154.

Berkhout, A. J., 1985, Seismic migration: Imaging of acoustic energy by wave field extrapolation: Elsevier, Amsterdam.

Chun, J. H., and Jacewitz, C. A., 1981, Fundamentals of frequency-domain migration: Geophysics, 46, no. 5, 717-733.

Claerbout, J. F., 1976, Fundamentals of geophysical data processing: Blackwell.

Claerbout, J. F., 1985, Imaging the Earth's Interior: Blackwell Scientific Publications.

Claerbout, J. F., 1986, Velocity extrapolation by cascaded fifteen degree migration: SEP-48, 79-84.

Claerbout, J. F., 1995, Basic Earth Imaging: Stanford Exploration Project.

Clayton, R. W., 1978, Common midpoint migration: SEP-14, 21-36.

Courant, R., 1962, Methods of mathematical physics: Interscience Publishers, New York.

Etgen, J., 1990, Residual prestack migration and interval velocity estimation: Ph.D. thesis, Stanford University.

Fomel, S., and Biondi, B., 1995, Azimuth moveout: the operator parameterization and antialiasing: SEP-89, 89-108.

Fomel, S. B., 1994, Method of velocity continuation in the problem of temporal seismic migration: Russian Geology and Geophysics, 35, no. 5, 100-111.

Fomel, S., 1995, Amplitude preserving offset continuation in theory, Part 1: The offset continuation equation: SEP-84, 179-198.

Fomel, S., 1996, Stacking operators: Adjoint versus asymptotic inverse: SEP-92, 267-292.

Fowler, P., 1988, Seismic velocity estimation using prestack time migration: Ph.D. thesis, Stanford University.

Gradshtein, I. S., and Ryzhik, I. M., 1994, Table of integrals, series, and products: Boston: Academic Press.

Jakubowicz, H., and Levin, S., 1983, A simple exact method of three-dimensional migration - Theory: Geophys. Prosp., 31, no. 1, 34-56.

Larner, K., and Beasley, C., 1987, Cascaded migrations - improving the accuracy of finite-difference migration: Geophysics, 52, no. 5, 618-643.

Levin, S., 1986a, Cascaded fifteen degree equations simplified: SEP-48, 101-108.

Levin, S., 1986b, Test your migration IQ: SEP-48, 147-160.

Li, Z., 1986, Cascaded one step fifteen degree migration versus Stolt migration: SEP-48, 85 -100.

Liptow, F., and Hubral, P., 1995, Migrating around in circles: The Leading Edge, 14, no. 11, 1125-1127.

Liu, Z., and Bleistein, N., 1995, Migration velocity analysis: Theory and iterative algorithm: Geophysics, 60, no. 1, 142-153.

MacKay, S., and Abma, R., 1992, Imaging and velocity estimation with depth-focusing analysis: Geophysics, 57, no. 12, 1608-1622.

Popovici, A. M., 1995, Prestack migration by split-step DSR: SEP-84, 53-60.

Rothman, D. H., Levin, S. A., and Rocca, F., 1985, Residual migration - applications and limitations: Geophysics, 50, no. 1, 110-126.

Schneider, W. A., 1978, Integral formulation for migration in two-dimensions and three-dimensions: Geophysics, 43, no. 1, 49-76.

Stolt, R. H., 1978, Migration by 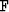$\mbox{F}$ourier transform: Geophysics, 43, no. 1, 23-48.

Tygel, M., Schleicher, J., and Hubral, P., 1994, Pulse distortion in depth migration: Geophysics, 59, no. 10, 1561-1569.

Yilmaz, O., and Chambers, R. E., 1984, Migration velocity analysis by wave-field extrapolation: Geophysics, 49, no. 10, 1664-1674.

Yilmaz, O., and Claerbout, J. F., 1980, Prestack partial migration: Geophysics, 45, no. 12, 1753-1779.

Yilmaz, O., 1979, Prestack partial migration: Ph.D. thesis, Stanford University.

A