




Next: INTEGRAL VELOCITY CONTINUATION AND
Up: Fomel: Velocity continuation
Previous: REFERENCES
The main goal of this appendix is to derive the partial differential
equation describing the image surface in a
depth-midpoint-offset-velocity space.
vlcray
Figure 11 Reflection rays in a constant
velocity medium (a scheme).
|
|  |

The derivation starts with observing a simple geometry of reflection
in a constant-velocity medium, shown in Figure 11. The
well-known equations for the apparent slowness
| 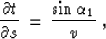 |
(64) |
| 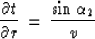 |
(65) |
relate the first-order traveltime derivatives for the reflected waves
to the emergency angles of the incident and reflected rays. Here s
stands for the source location at the surface, r is the receiver
location, t is the reflection traveltime, v is the constant
velocity, and 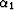 and
and 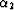 are the angles shown in Figure
11. Considering the traveltime derivative with respect to
the depth of the observation surface z, we can see that the
contributions of the two branches of the reflected ray, added
together, form the equation
are the angles shown in Figure
11. Considering the traveltime derivative with respect to
the depth of the observation surface z, we can see that the
contributions of the two branches of the reflected ray, added
together, form the equation
| 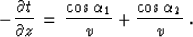 |
(66) |
It is worth mentioning that the elimination of angles from equations
(64), (65), and (66) leads to the famous
double-square-root equation,
| 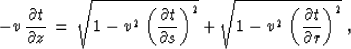 |
(67) |
published in the Russian literature by Belonosova and Alekseev
1967 and commonly used in the form of a
pseudo-differential dispersion relation
Claerbout (1985); Clayton (1978) for prestack migration
Popovici (1995); Yilmaz (1979). Considered locally,
equation (67) is independent of the constant velocity assumption
and enables prestack downward continuation of reflected waves in
heterogeneous media.
Introducing midpoint coordinate 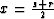 and half-offset
and half-offset
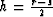 , we can apply the chain rule and elementary
trigonometric equalities to formulas (64) and
(65) and transform these formulas to
, we can apply the chain rule and elementary
trigonometric equalities to formulas (64) and
(65) and transform these formulas to
| 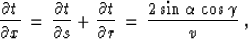 |
(68) |
| 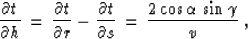 |
(69) |
where 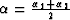 is the dip angle, and
is the dip angle, and
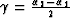 is the reflection angle
Claerbout (1985); Clayton (1978). Equation
(66) transforms analogously to
is the reflection angle
Claerbout (1985); Clayton (1978). Equation
(66) transforms analogously to
| 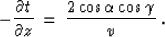 |
(70) |
This form of equation (66) is used to describe the stretching
factor of the waveform distortion in depth migration Tygel et al. (1994).
Dividing (68) and (69) by (70), we obtain
| 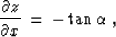 |
(71) |
| 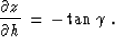 |
(72) |
Substituting formulas (71) and (72) into equation
(70) yields yet another form of the double-square-root equation:
| 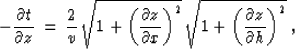 |
(73) |
which is analogous to the dispersion relationship of Stolt prestack
migration Stolt (1978).
The law of sines in the triangle formed by the incident and reflected
ray leads to the explicit relationship between the traveltime and the
offset:
| 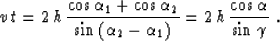 |
(74) |
The combination of formulas (74), (68), and
(69) forms the basic kinematic equation of the offset
continuation theory Fomel (1995):
| 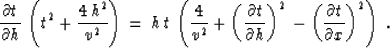 |
(75) |
Differentiating (74) with respect to the velocity v yields
| 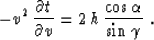 |
(76) |
Finally, dividing (76) by (70), we get
| 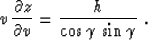 |
(77) |
Equation (77) can be written in a variety of ways with the help
of an explicit geometric relationship between the half-offset h and
the depth z,
| 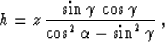 |
(78) |
which follows directly from the trigonometry of the triangle in
Figure 11 Fomel (1995). For example, equation
(77) can be transformed to the form obtained recently by Liu and
Bleistein 1995:
| 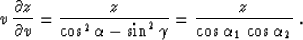 |
(79) |
In order to separate different factors contributing to the velocity
continuation process, we can transform this equation to the form
| 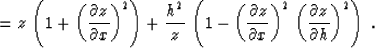 |
(80) |
Rewritten in terms of the vertical traveltime, it further transforms
to equation (1) in the main text. Yet another form of the
kinematic velocity continuation equation follows from eliminating the
reflection angle 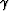 from equations (77) and (78). The
resultant expression takes the following form:
from equations (77) and (78). The
resultant expression takes the following form:
| 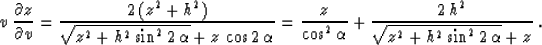 |
(81) |
B





Next: INTEGRAL VELOCITY CONTINUATION AND
Up: Fomel: Velocity continuation
Previous: REFERENCES
Stanford Exploration Project
11/12/1997


![]() and half-offset
and half-offset
![]() , we can apply the chain rule and elementary
trigonometric equalities to formulas (64) and
(65) and transform these formulas to
, we can apply the chain rule and elementary
trigonometric equalities to formulas (64) and
(65) and transform these formulas to