|
adjcon
Figure 1 Comparison of convergence of the iterative inversion with different DMO operators. The relative squared residual error is plotted against the number of iteration. | 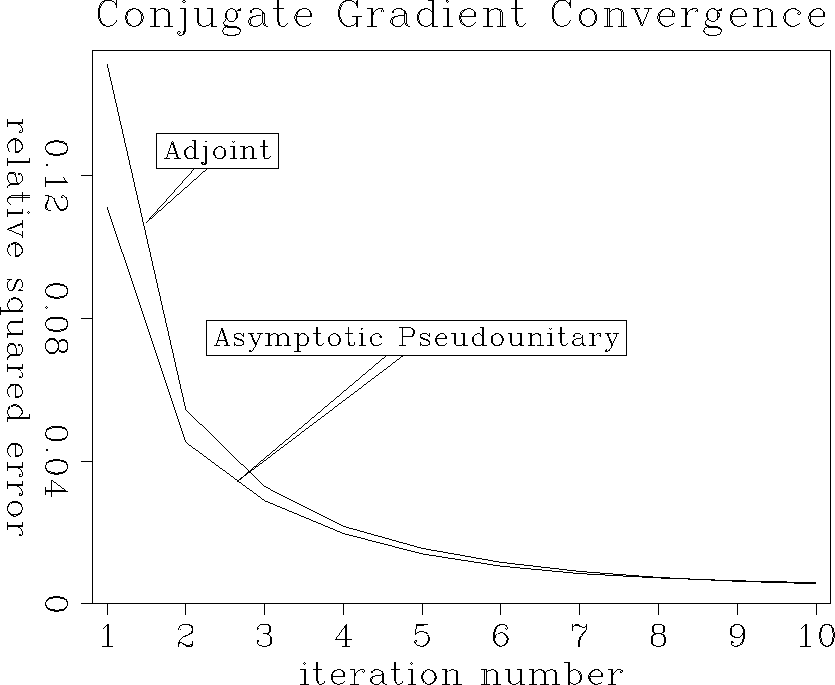 |
|
adjcon
Figure 1 Comparison of convergence of the iterative inversion with different DMO operators. The relative squared residual error is plotted against the number of iteration. |  |
 |
 |
 |
 |
 |
 |