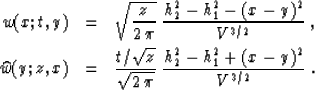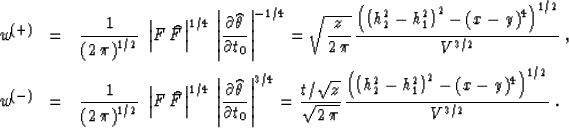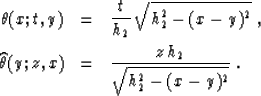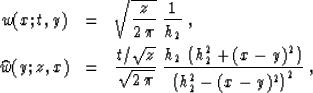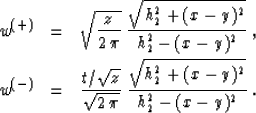Next: NUMERIC TEST
Up: EXAMPLES
Previous: Velocity Transform
Offset continuation is the operator that transforms seismic reflection
data from one offset to another
Bolondi et al. (1982); Salvador and Savelli (1982). If the data are continued
from half-offset h1 to a larger offset h2, the summation path of
the post-NMO integral offset continuation has the following form
Biondi and Chemingui (1994); Fomel (1995b); Stovas and Fomel (1996):
| 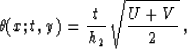 |
(85) |
where U = h12 + h22 - (x - y)2, 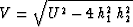 , and x and y are the midpoint coordinates before and
after the continuation. The summation path of the reverse continuation
is found from inverting (85) to be
, and x and y are the midpoint coordinates before and
after the continuation. The summation path of the reverse continuation
is found from inverting (85) to be
| 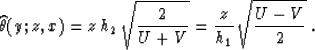 |
(86) |
The Jacobian of the time coordinate transformation in this case is simply
| 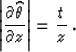 |
(87) |
Differentiating summation paths (85) and (86), we
can define the product of the weighting functions according to formula
(9), as follows:
| 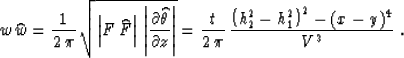 |
(88) |
The weighting functions of the amplitude-preserving offset
continuation have the form![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
| 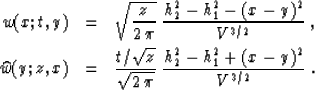 |
(89) |
| (90) |
It easy to verify that they satisfy relationship (88);
therefore, they appear to be asymptotically inverse to each other.
The weighting functions of the asymptotic pseudo-unitary offset
continuation are defined from formulas (34) and (35), as follows:
| 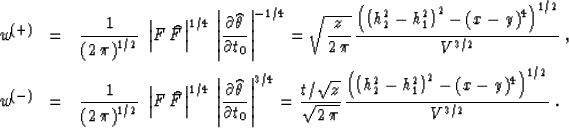 |
(91) |
| (92) |
The most important case of offset continuation is the continuation
to zero offset. This type of continuation is known as dip moveout
(DMO). Setting the initial offset h1 equal to zero in the general
offset continuation formulas, we deduce that the inverse and forward
DMO operators have the summation paths
| 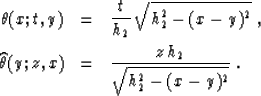 |
(93) |
| (94) |
The weighting functions of the amplitude-preserving inverse and
forward DMO are
| 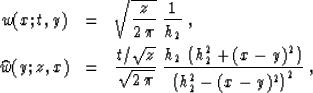 |
(95) |
| (96) |
and the weighting functions of the asymptotic pseudo-unitary DMO are
| 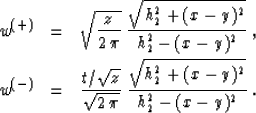 |
(97) |
| (98) |
Formulas similar to (95) and (96) have been published
by Fomel 1995b and Stovas and Fomel
1996. Formula (96) differs from the
similar result of Black et al. 1993 by a simple time
multiplication factor. This difference corresponds to the difference
in definition of the amplitude preservation criterion. Formula
(96) agrees asymptotically with the frequency-domain Born DMO
operators Bleistein and Cohen (1995); Bleistein (1990). Likewise, the stacking operator with the
weighting function (95) corresponds to Ronen's inverse DMO
Ronen (1987), as I discussed in an earlier report
Fomel (1995b). Its adjoint, which has the weighting function
| 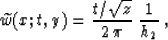 |
(99) |
corresponds to Hale's DMO Hale (1984).





Next: NUMERIC TEST
Up: EXAMPLES
Previous: Velocity Transform
Stanford Exploration Project
11/12/1997
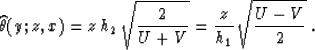
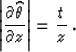
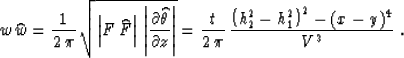
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)