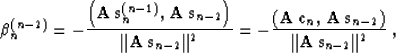Next: Induction
Up: IN SEARCH OF THE
Previous: First step of the
Now let us assume n > 2 and add some amount of the step from
the (n-2)-th iteration to the search direction, determining the new
direction 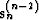 , as follows:
, as follows:
| 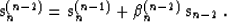 |
(17) |
We can deduce that after the second change, the value of numerator in
equation (9) is still the same:
| ![\begin{displaymath}
\left({\bf r}_{n-1},\,{\bf A\,s}_n^{(n-2)}\right)^2 = \left[...
...ight)\right]^2 =
\left({\bf r}_{n-1},\,{\bf A\,c}_n\right)^2\;.\end{displaymath}](img34.gif) |
(18) |
This remarkable fact occurs as the result of transforming the dot product 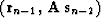 with the help of equation
(4):
with the help of equation
(4):
| 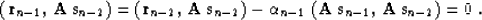 |
(19) |
The first term in (19) is equal to zero according to formula
(7); the second term is equal to zero according to formula
(15). Thus we have proved the new orthogonality equation
| 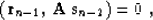 |
(20) |
which in turn leads to the numerator invariance (18). The
value of the coefficient 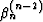 in (17) is defined
analogously to (14) as
in (17) is defined
analogously to (14) as
| 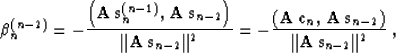 |
(21) |
where we have again used equation (15). If 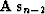 is
not orthogonal to
is
not orthogonal to 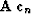 , the second step of the improvement leads
to a further decrease of the denominator in (8) and,
consequently, to a further decrease of the residual.
, the second step of the improvement leads
to a further decrease of the denominator in (8) and,
consequently, to a further decrease of the residual.





Next: Induction
Up: IN SEARCH OF THE
Previous: First step of the
Stanford Exploration Project
11/12/1997