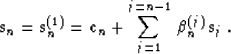Next: ALGORITHM
Up: IN SEARCH OF THE
Previous: Second step of the
Continuing by induction the process of adding a linear combination of
the previous steps to the arbitrarily chosen direction 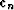 (known in mathematics as the Gram-Schmidt orthogonalization
process), we finally arrive at the complete definition of the new
step
(known in mathematics as the Gram-Schmidt orthogonalization
process), we finally arrive at the complete definition of the new
step 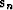 , as follows:
, as follows:
| 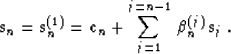 |
(22) |
Here the coefficients 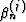 are defined by equations
are defined by equations
| 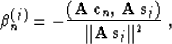 |
(23) |
which correspond to the orthogonality principles
| 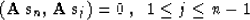 |
(24) |
and
| 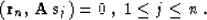 |
(25) |
It is these orthogonality properties that allowed us to optimize the
search parameters one at a time instead of solving the n-dimensional
system of optimization equations for 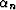 and
and 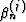 .
.





Next: ALGORITHM
Up: IN SEARCH OF THE
Previous: Second step of the
Stanford Exploration Project
11/12/1997