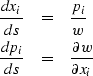
The ray tracing method I have implemented is based on the ray tracing system of first-order partial-differential equations, derived from the Eikonal equation by the method of characteristics (see Cerveny1987 for more details):
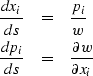 |
||
| (37) |
| |
(38) |
The slowness vector is perpendicular to the wavefront
(![]() ), and must satisfy
), and must satisfy
| (39) |
The system of ray equations together with equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
can be solved by a standard numerical integration method.
I use a fourth-order Rungge-Kutta method.
It propagates the properties of the ray (xi,pi, and t) over
an increment in arclength by combining the information
from several Euler-style steps (each involving one evaluation of
the right-hand side of equations (
)
can be solved by a standard numerical integration method.
I use a fourth-order Rungge-Kutta method.
It propagates the properties of the ray (xi,pi, and t) over
an increment in arclength by combining the information
from several Euler-style steps (each involving one evaluation of
the right-hand side of equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )),
and then uses the information
obtained to match a fourth-order Taylor series expansion
of the ray variables at the current position.
)),
and then uses the information
obtained to match a fourth-order Taylor series expansion
of the ray variables at the current position.
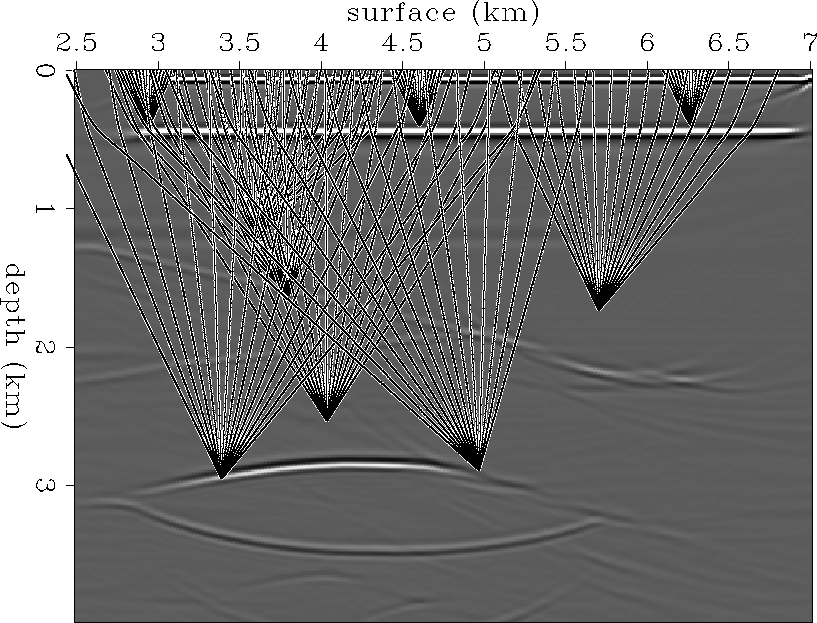
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows some of rays traced
through the reference model shown in Figure
shows some of rays traced
through the reference model shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
 |