A method for restoring missing data is to regenerate from the model that fits to the known data. Since all reflection events are hyperbolic in CMP gathers, CMP gathers provide a good model for missing traces. Therefore, if we find the velocity spectrum that most closely produces the known data in a CMP gather, we can predict the missing data by hyperbolic modeling from the velocity spectrum.
Thus, the interpolation of missing near offset traces can be achieved in two steps. The first step is to find the best velocity spectrum from the known traces in each CMP gather. The search for the optimum velocity spectrum in the CMP gather can be formulated in a least-squares sense, as
| (20) |
The second step is to model the missing traces from the optimum velocity spectrum, as follows:
| (21) |
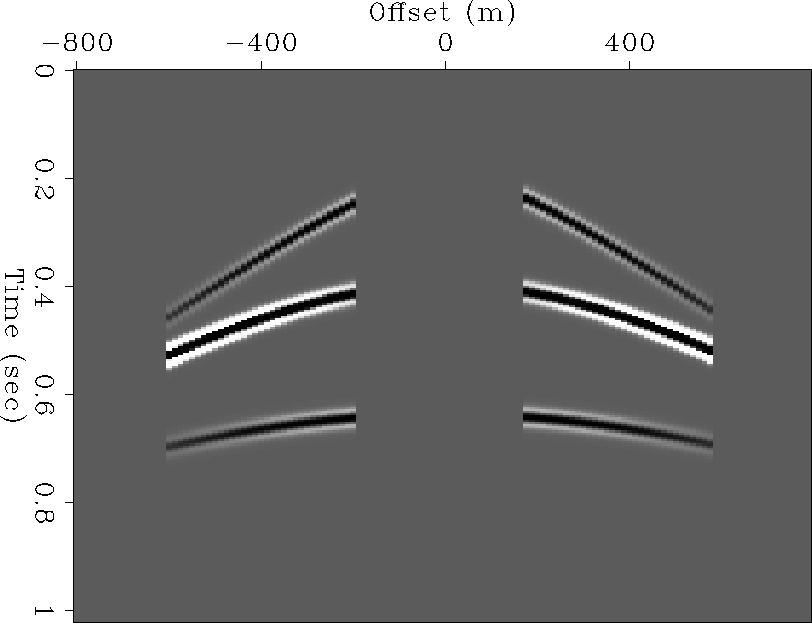
I have tested a simple synthetic CMP gather
to verify the approach explained in the above.
First, I put three spikes in a velocity spectrum
and modeled a CMP gather by spreading the spectrum energy along
the hyperbola,
and then convolved the CMP gather with a Ricker wavelet
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Figure
).
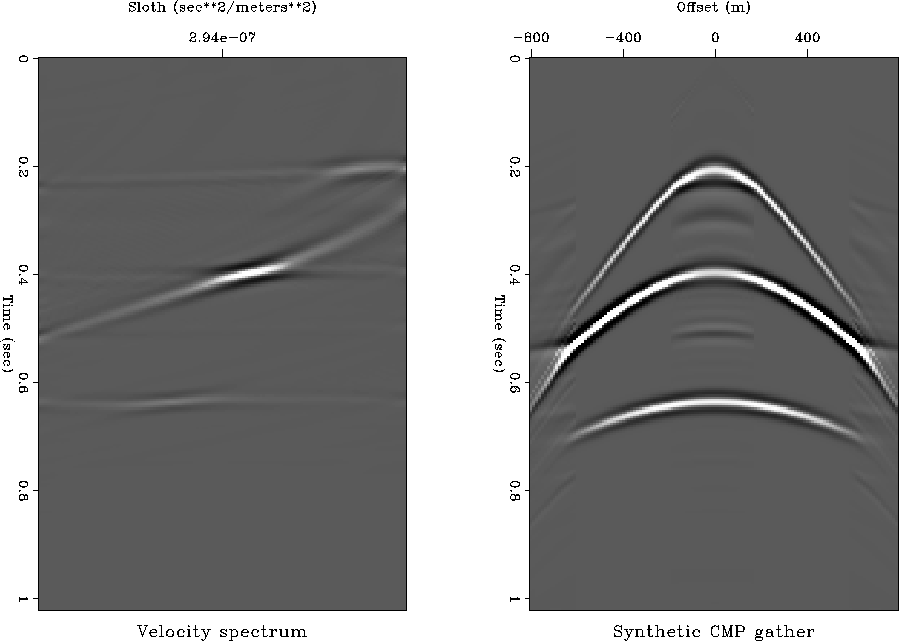
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the interpolated CMP gather using
the least-squares conjugate gradient algorithm.
Because of the smoothness of the optimum velocity
spectrum found by the least-squares method,
the interpolated traces are close to the other traces
in the near offset but not in the far offset.
shows the interpolated CMP gather using
the least-squares conjugate gradient algorithm.
Because of the smoothness of the optimum velocity
spectrum found by the least-squares method,
the interpolated traces are close to the other traces
in the near offset but not in the far offset.
In order to make the interpolated traces close to the other known traces, we need an optimum velocity spectrum which is spikier. To make the optimum velocity spectrum spiker, I used an adaptive weighting factor in the conjugate gradient. The velocity spectrum of the preceding step in each iteration is a good candidate for this problem, because the velocity spectrum has a larger value where we want to make the spiky spectrum than elsewhere after the first iteration. Thus, we solve the following iteratively-reweighted least-squares problem,
| |
(22) |
Wi = | mi-1 |.
In equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the subscript i represents
the iteration step in the conjugate gradient.
Figure
), the subscript i represents
the iteration step in the conjugate gradient.
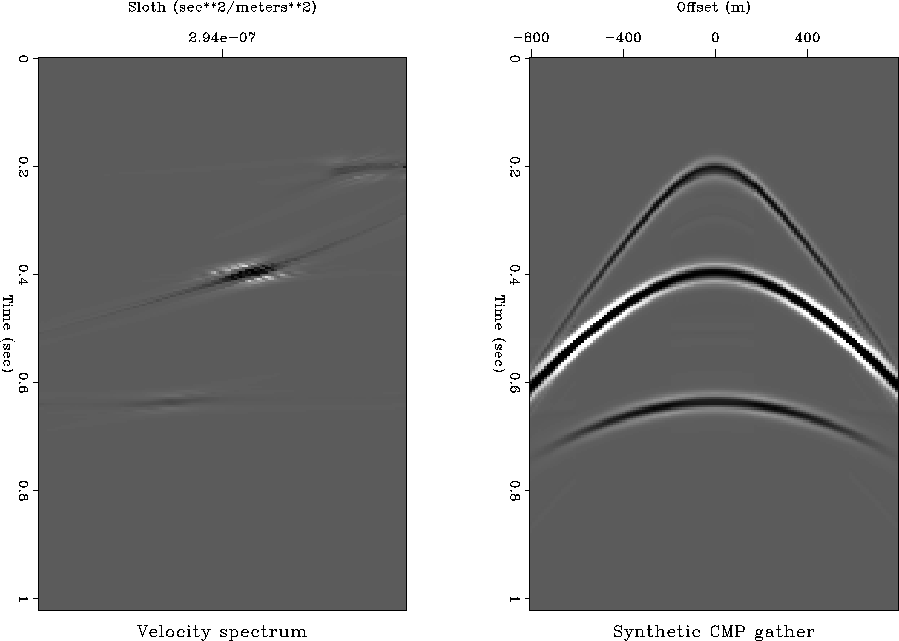
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the interpolated CMP gather
by using the adaptive weight least-squares method.
Now we have an interpolated trace in the near and far offset
that is closer to the known trace.
shows the interpolated CMP gather
by using the adaptive weight least-squares method.
Now we have an interpolated trace in the near and far offset
that is closer to the known trace.
 |
 |
 |