




Next: SYNTHETIC EXAMPLE
Up: Harlan: Flexible tomography
Previous: VELOCITY PERTURBATIONS
For this application, I found it advantageous
to write a generic ``Gauss-Newton'' optimization routine that
minimizes a least-squares objective function
with a non-linear forward model.
Both ray tracing and tomographic inversion of velocities
are optimized with this algorithm. The ray parameters in equation
(7) are perturbed until the traveltime is minimized.
(The traveltime is a nonlinear function of local velocities.)
The error between picked and modeled traveltimes (9)
is minimized by perturbations of velocity parameters (4).
In each case, a model damping term is included for numerical
stability.
Let the vector 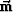 describe a model, and a vector
describe a model, and a vector 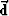 contain the data whose errors will be minimized.
Define also a scalar product for each of
these vectors:
contain the data whose errors will be minimized.
Define also a scalar product for each of
these vectors:
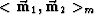 and
and
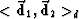 .The squared magnitude of each is defined by
.The squared magnitude of each is defined by
| 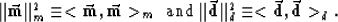 |
(11) |
These scalar products incorporate any non-stationary variances or
covariances that can be assumed for the problem. For
example, I will be assuming smaller variances for higher-order
polynomials used to describe raypaths.
The velocity parameters  and
and  will have small
variances on the order of 0.05, and the velocity Vx will
depend on the physical units of the survey.
Rather than introduce correlations between samples into
the scalar product, I prefer to encourage such correlations
with the choice of basis functions. By scaling basis
functions correctly, we can make the model norms
become the trivial Cartesian norm, simply summing the squares
of model parameters. I do not assume any correlation
in the errors of traveltime data.
will have small
variances on the order of 0.05, and the velocity Vx will
depend on the physical units of the survey.
Rather than introduce correlations between samples into
the scalar product, I prefer to encourage such correlations
with the choice of basis functions. By scaling basis
functions correctly, we can make the model norms
become the trivial Cartesian norm, simply summing the squares
of model parameters. I do not assume any correlation
in the errors of traveltime data.
Assume we wish to fit the data 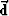 with
a non-linear forward model
with
a non-linear forward model 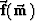 .We also must apply a linearized forward transform
.We also must apply a linearized forward transform
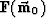 for a given
reference model
for a given
reference model 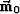 , so that
, so that
| 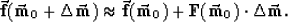 |
(12) |
We must be able to apply the transforms 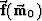 and
and 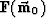 when necessary and apply
the adjoint
when necessary and apply
the adjoint
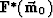 of the linear transform, defined by
of the linear transform, defined by
| 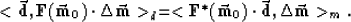 |
(13) |
Let us assume that all optimum models 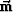 can then be specified to minimize an objective function
of the form
can then be specified to minimize an objective function
of the form
| 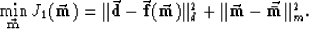 |
(14) |
where 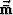 contains the expected mean of the model.
The relative weighting of the two terms ideally should
be equal when covariances are included properly in the
dot products. To optimize a raypath I minimize the traveltime.
To optimize velocities I minimize the differences
between measured and modeled traveltimes.
contains the expected mean of the model.
The relative weighting of the two terms ideally should
be equal when covariances are included properly in the
dot products. To optimize a raypath I minimize the traveltime.
To optimize velocities I minimize the differences
between measured and modeled traveltimes.
The objective function is iteratively approximated
by a quadratic objective function, using the
linearized forward model
| 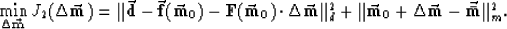 |
(15) |
This quadratic objective function is easily optimized
by a gradient method such as conjugate gradients.
The gradient
| 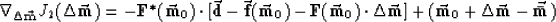 |
(16) |
requires application of the adjoint linearized transform.
The resulting linearized perturbation is added to the
reference model, after optimizing a scale factor 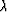 by
a line search:
by
a line search:
| 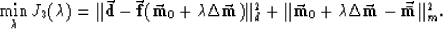 |
(17) |
The reference model is updated by the scaled perturbation, the
transform is relinearized, and the new quadratic (15) is
optimized again, until convergence.





Next: SYNTHETIC EXAMPLE
Up: Harlan: Flexible tomography
Previous: VELOCITY PERTURBATIONS
Stanford Exploration Project
11/12/1997
![]() describe a model, and a vector
describe a model, and a vector ![]() contain the data whose errors will be minimized.
Define also a scalar product for each of
these vectors:
contain the data whose errors will be minimized.
Define also a scalar product for each of
these vectors:
![]() and
and
![]() .The squared magnitude of each is defined by
.The squared magnitude of each is defined by
![]() with
a non-linear forward model
with
a non-linear forward model ![]() .We also must apply a linearized forward transform
.We also must apply a linearized forward transform
![]() for a given
reference model
for a given
reference model ![]() , so that
, so that